
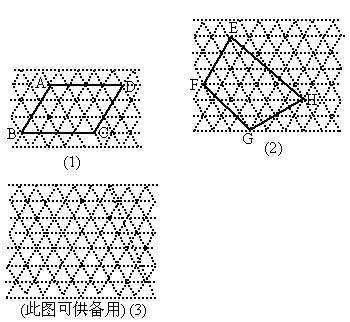
如图所示,图中的虚线网格我们称之为正三角形网格.它的每一个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形.
(1)直接写出单位正三角形的高与面积.
(2)图(1)中的 ABCD含有多少个单位正三角形?
ABCD含有多少个单位正三角形? ABCD的面积是多少?
ABCD的面积是多少?
(3)求出图(1)中线段AC的长(可作辅助线).
(4)求出图(2)中四边形EFGH的面积.

|
解: (1)单位正三角形的高为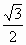 ,面积为 ,面积为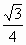 . .
(2) 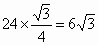 . .
(3) 过点A作AK⊥BC于K(如图所示).
在 Rt△ACK中,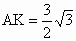 , ,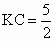 . .
所以 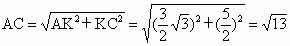 . .
(4) 解法一:如图所示,将四边形EFGH分割成五部分,以FG为对角线构造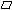 FPGM. FPGM.
所以 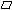 FPGM中含有6个单位正三角形,所以 FPGM中含有6个单位正三角形,所以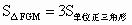 . .
同理可得到其他四部分面积.所以
解法二:如图所示,构造 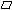 EQSR.过点F作FT⊥QG于T,则 EQSR.过点F作FT⊥QG于T,则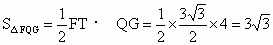 .同理可求 .同理可求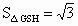 , ,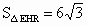 , ,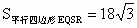 . .
|
(1)利用等边三角形的性质和勾股定理求出高与面积. (2) (3)要求AC的长,构造直角三角形,应用勾股定理求出. (4)要求四边形EFGH的面积,先将其分割,然后求每部分的面积,再相加和即可. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:数学教研室 题型:044
如图所示,图中的虚线网格我们称之为正三角形网格.它的每一个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形.
(1)直接写出单位正三角形的高与面积.
(2)图(1)中的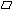 ABCD含有多少个单位正三角形?
ABCD含有多少个单位正三角形?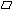 ABCD的面积是多少?
ABCD的面积是多少?
(3)求出图(1)中线段AC的长(可作辅助线).
(4)求出图(2)中四边形EFGH的面积.
查看答案和解析>>
科目:初中数学 来源:黄冈难点课课练 七年级数学下册(北师大版) 题型:013
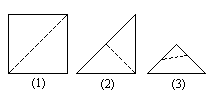
如图所示,小华拿张正方形的纸,沿虚线对折一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线剪下去一个角,再打开后的形状是
[ ]
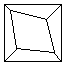
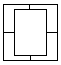
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长
方形,再按图2围成一个较大的正方形.
 |
(1)请用两种方法表示图2中阴影部分的面积(只需表示,不必化简);
(2)比较(1)的两种结果,你能得到怎样的等量关系?
(3)请你用(2)中得到的等量关系解决下面问题:如果m-n=4,mn=12,求m+n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长
方形,再按图2围成一个较大的正方形.
 |
(1)请用两种方法表示图2中阴影部分的面积(只需表示,不必化简);
(2)比较(1)的两种结果,你能得到怎样的等量关系?
(3)请你用(2)中得到的等量关系解决下面问题:如果m-n=4,mn=12,求m+n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com