解:(1)∵点A(4,m)在反比例函数y=
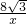
的图象上,
∴m=
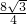
=2

,
∴点A的坐标为(4,2

),
∵点A(4,2

),点E(0,-2

)都在直线y=kx+b上,
∴
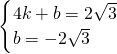
,
解得
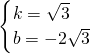
,
∴直线解析式为y=

x-2

,
令y=0,则

x-2

=0,
解得x=2,
∴点C的坐标为(2,0);
(2)y轴上存在点D(0,2

),使CD=DA.
理由如下:设点D的坐标为(0,y),
则CD=
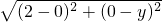
,
AD=
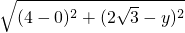
,
∵CD=DA,
∴
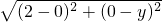
=
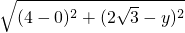
,
两边平方并整理得,4

y-24=0,
解得y=2

,
∴y轴上存在点D(0,2

),使CD=DA;
(3)结论①PE
2+PF
2=PC
2正确.
理由如下:∵点C坐标为(2,0),点E坐标为(0,-2

),
∴CE=
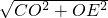
=
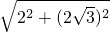
=4,tan∠ECO=
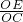
=
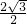
=

,
∴∠ECO=60°,
又∵点F、C关于y轴对称,
∴FC=2+2=4,
∴FC=CE,
∴△CEF是等边三角形,
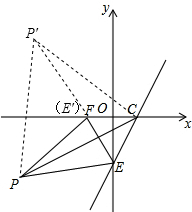
如图,把△PCE绕点C顺时针旋转60°得到△P′C′E,连接PP′,
则点E与点F重合,△PP′C为等边三角形,
根据三角形的外角性质,∠PFP′=∠CPF+∠CP′E′+∠PCP′,
=∠CPF+∠CPE+∠PCP′
=∠EPF+∠PCP′,
∵∠EPF=30°,
∴∠PFP′=30°+60°=90°,
∴△PFP′是直角三角形,
即P′E′
2+PF
2=PP′
2,
∴PE
2+PF
2=PC
2.
故结论①正确,结论②错误.
分析:(1)把点A的坐标代入反比例函数解析式求出m的值,再利用待定系数法求一次函数解析式求出直线的解析式,然后令y=0,求解即可得到点C的坐标;
(2)设点D的坐标为(0,y),利用两点间的距离公式列式进行计算,如果方程有解,则存在,否则不存在;
(3)先求出△CEF是等边三角形,再把△PCE绕点C顺时针旋转60°得到△P′C′E,连接PP′,则△PP′C为等边三角形,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠PFP′=∠EPF+∠PCP′=90°,再根据勾股定理可得P′E′
2+PF
2=PP′
2,也就是PE
2+PF
2=PC
2,从而得到第一个结论正确,第二个结论错误.
点评:本题综合考查了反比例函数的问题,主要利用了点在反比例函数图象上,待定系数法求一次函数解析式,两点间的距离公式,旋转变换的性质,等边三角形的判定与性质,以及勾股定理的应用,综合性较强,难度较大,(3)利用旋转变换和三角形的外角性质把∠EPF=30°与60°的角转化为一个直角从而得到直角三角形是解题的关键.

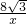 的图象于点A(4,m)和点B,交x轴于点C,交y轴于点E(0,-2
的图象于点A(4,m)和点B,交x轴于点C,交y轴于点E(0,-2 )
)
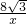 的图象上,
的图象上,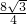 =2
=2 ,
, ),
), ),点E(0,-2
),点E(0,-2 )都在直线y=kx+b上,
)都在直线y=kx+b上,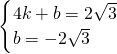 ,
,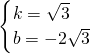 ,
, x-2
x-2 ,
, x-2
x-2 =0,
=0, ),使CD=DA.
),使CD=DA.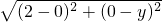 ,
,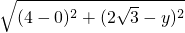 ,
,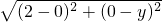 =
=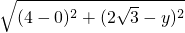 ,
, y-24=0,
y-24=0, ,
, ),使CD=DA;
),使CD=DA; ),
),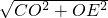 =
=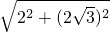 =4,tan∠ECO=
=4,tan∠ECO=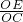 =
=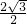 =
= ,
,


 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式