Question

【题目】如图，矩形ABCD中，AB=3，AD=4，E为AB上一点，AE=1，M为射线AD上一动点，AM=a（a为大于0的常数），直线EM与直线CD交于点F，过点M作MG⊥EM，交直线BC于点G．

（1）若M为边AD中点，求证△EFG是等腰三角形；
（2）若点G与点C重合，求线段MG的长；
（3）请用含a的代数式表示△EFG的面积S，并指出S的最小整数值．

Answer 1

【答案】
（1）

证明：∵四边形ABCD是矩形，

∴∠A=∠MDF=90°，

∵M为边AD中点，

∴MA=MD

在△MAE和△MDF中，

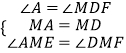
∴△MAE≌△MDF（ASA），

∴EM=FM，

又∵MG⊥EM，

∴EG=FG，

∴△EFG是等腰三角形；

（2）

解：如图1，

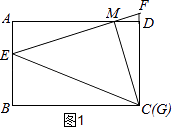
∵AB=3，AD=4，AE=1，AM=a

∴BE=AB﹣AE=3﹣1=2，BC=AD=4，

∴EM2=AE2+AM2，EC2=BE2+BC2，

∴EM2=1+a2，EC2=4+16=20，

∵CM2=EC2﹣EM2，

∴CM2=20﹣1﹣a2=19﹣a2，

∴CM= ．

∵AB∥CD，

∴∠AEM=∠MFD，

又∵∠MCD+∠MFD=90°，∠AME+∠AEM=90°，

∴∠AME=∠MCD，

∵∠MAE=∠CDM=90°，

∴△MAE∽△CDM，

∴ = ，即 = ，

解得a=1或3，

代入CM= ．

得CM=3 或 ．

（3）

解：①当点M在AD上时，如图2，作MN⊥BC，交BC于点N，

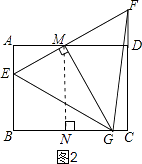
∵AB=3，AD=4，AE=1，AM=a

∴EM= = ，MD=AD﹣AM=4﹣a，

∵∠A=∠MDF=90°，∠AME=∠DMF，

∴△MAE∽△MDF

∴ = ，

∴ = ，

∴FM= ，

∴EF=EM+FM= + = ，

∵AD∥BC，

∴∠MGN=∠DMG，

∵∠AME+∠AEM=90°，∠AME+∠DMG=90°，

∴∠AME=∠DMG，

∴∠MGN=∠AEM，

∵∠MNG=∠MAE=90°，

∴△MNG∽△MAE

∴ = ，

∴ = ，

∴MG= ，

∴S= EFMG= × × = +6，

即S= +6，

当a= 时，S有最小整数值，S=1+6=7．

②当点M在AD的延长线上时，如图3，作MN⊥BC，交BC延长线于点N，

∵AB=3，AD=4，AE=1，AM=a

∴EM= = ，MD=a﹣4，

∵DC∥AB，

∴△MAE∽△MDF

∴ = ，

∴ = ，

∴FM= img src="http://thumb.zyjl.cn/questionBank/Upload/2017/08/15/10/03a9f863/SYS201708151049289122374001_DA/SYS201708151049289122374001_DA.012.png" width="57" height="25" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ，

∴EF=EM﹣FM= ﹣ = ，

∵∠AME+∠EMN=90°，∠NMG+∠EMN=90°，

∴∠AME=∠NMG，

∵∠MNG=∠MAE=90°，

∴△MNG∽△MAE

∴ = ，

∴ = ，

∴MG= ，

∴S= EFMG= × × = +6，

即S= +6，

当a＞4时，S没有整数值．

综上所述当a= 时，S有最小整数值，S=1+6=7．

【解析】（1）利用△MAE≌△MDF，求出EM=FM，再由MG⊥EM，得出EG=FG，所以△EFG是等腰三角形；（2）利用勾股定理EM2=AE2+AM2 ， EC2=BE2+BC2 ， 得出CM2=EC2﹣EM2 ， 利用线段关系求出CM．再△MAE∽△CDM，求出a的值，再求出CM．（3）①当点M在AD上时，②：①当点M在AD的延长线上时，作MN⊥BC，交BC于点N，先求出EM，再利用△MAE∽△MDF求出FM，得到EF的值，再由△MNG∽△MAE得出MG的长度，然后用含a的代数式表示△EFG的面积S，指出S的最小整数值．
【考点精析】本题主要考查了相似三角形的性质的相关知识点，需要掌握对应角相等，对应边成比例的两个三角形叫做相似三角形才能正确解答此题．