
如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则以AC和BC的长为两根的一元二次方程是( )
A. | B. |
C. | D. |
A.
解析试题分析:连接AD,BD,OD,由AB为直径与四边形DCFE是正方形,即可证得△ACD∽△DCB,则可求得AC•BC=DC2=1,又由勾股定理求得AB的值,即可得AC+BC=AB,根据根与系数的关系即可求得答案.
连接AD,BD,OD,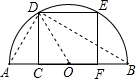
∵AB为直径,
∴∠ADB=90°,
∵四边形DCFE是正方形,
∴DC⊥AB,
∴∠ACD=∠DCB=90°,
∴∠ADC+∠CDB=∠A+∠ADC=90°,
∴∠A=∠CDB,
∴△ACD∽△DCB,
∴ ,
,
又∵正方形CDEF的边长为1,
∵AC•BC=DC2=1,
∵AC+BC=AB,
在Rt△OCD中,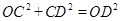 ,
,
∴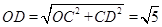 ,
,
∴AC+BC=AB=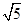 ,
,
以AC和BC的长为两根的一元二次方程是
考点:(1)根与系数的关系;(2)勾股定理;(3)正方形的性质;(4)圆周角定理;(5)相似三角形的判定与性质.


科目:初中数学 来源: 题型:单选题
已知△ABC和△DEF相似,且△ABC的三边长为3、4、5,如果△DEF的周长为6,那么下列不可能是△DEF一边长的是( )
| A.1.5; | B.2; | C.2.5; | D.3. |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,D是△ABC的边BC上一点,已知AB=4,AD=2.∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为( )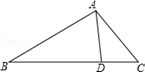
| A.a | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为
A、 B、(m,n) C、
B、(m,n) C、 D、
D、
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
两地实际距离为2000米,图上距离为2cm,则这张地图的比例尺为( )
| A.1000:1 | B.100000:1 | C.1:1000 | D.1:100000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com