Question

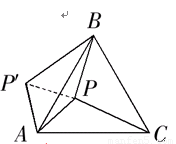
如图，P是正三角形ABC 内的一点，且PA＝6，PB＝8，PC＝10。若将△PAC绕点A逆时针旋转后，得到△P^/AB。⑴求点P与点P′之间的距离；⑵∠APB的度数。

 

Answer 1

【答案】

（1）由题意可知BP′=PC＝10，AP′=AP，∠PAC＝P^/AB，……………3分

∵∠PAC＋∠BAP＝60°

∴∠PAP′＝60°                          

∴△APP′为等边三角形

∴PP′＝AP＝AP′＝6                   ………………………5分

（2）∵PP^/2＋BP²＝BP^/2

∴△BPP′为直角三角形，且∠BPP′＝90°……………………………8分

∴∠APB＝90°＋60°＝150°。                 ……………………10 分

【解析】（1）由已知△PAC绕点A逆时针旋转后，得到△P′AB，可得△PAC≌△P′AB，PA=P'A，旋转角∠P'AP=∠BAC=60°，∴△APP'为等边三角形，即可求得PP'；

（2）由△APP'为等边三角形，得∠APP'=60°，在△PP'B中，已知三边，用勾股定理逆定理证出直角三角形，得出∠P'PB=90°，可求∠APB的度数．