Question

若等腰三角形两边长分别为4和6，则底边上的高等于

1. A.
   或
2. B.
   或
3. C.
   
4. D.
   

Answer 1

A
分析：因为题目没有说明哪个边为腰哪个边为底，所以需要讨论，①当4为腰时，此时等腰三角形的边长为4、4、6；②当6为腰时，此时等腰三角形的边长为4、6、6；然后根据等腰三角新的高垂直平分底边可运用解直角三角形的知识求出高．
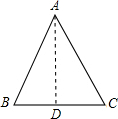
解答：解：
∵AB=AC，AD⊥BC，
∴BD=CD，
边长为4、6的等腰三角形有4、4、6与4、6、6两种情况，
①当是4、4、6时，底边上的高AD===；
②当是4、6、6时，同理求出底边上的高AD是=．
故选A．
点评：本题考查勾股定理及等腰三角形的性质，解答本题需要掌握三点，①等腰三角新的高垂直平分底边；②勾股定理的表达式；③三角形的三边关系．