
如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.
(1)判断△ABC和△DEF是否相似,并说明理由;
(2)P1,P2,P3,P4,P5,D,F是△DEF边上的7个格点,请在这7个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似(要求写出2个符合条件的三角形,并在图中连结相应线段,不必说明理由).
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
如图,矩形ABCD中,AD=3厘米,AB=a厘米(a>3).动点M,N同时从B点出发,分别沿B?A,B?C运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于P,Q.当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.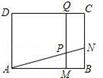
(1)若a=4厘米,t=1秒,则PM= _________ 厘米;
(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围;
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形PMBN,梯形PQDA,梯形PQCN的面积都相等?若存在,求a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读下面的材料:
小明遇到一个问题:如图(1),在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G. 如果 ,求
,求 的值.
的值. 
他的做法是:过点E作EH∥AB交BG于点H,则可以得到△BAF∽△HEF.
请你回答:(1)AB和EH的数量关系为 ,CG和EH的数量关系为 , 的值为 .
的值为 .
(2)如图(2),在原题的其他条件不变的情况下,如果 ,那么
,那么 的值为 (用含a的代数式表示).
的值为 (用含a的代数式表示).
(3)请你参考小明的方法继续探究:如图(3),在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果 ,那么
,那么 的值为 (用含m,n的代数式表示).
的值为 (用含m,n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米.求路灯的高.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡角 为
为 ,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为500米.
,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为500米.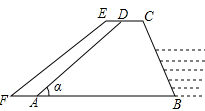
(1)求完成该工程需要多少立方米方土?
(2)某工程队在加固600立方米土后,采用新的加固模式,这样每天加固方数是原来的2倍,结果只用11天完成了大坝加固的任务.请你求出该工程队原来每天加固多少立方米土?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上一点(不与点A、B重合),连结CO并延长CO交⊙O于点D,连结AD.
(1)求弦长AB的长度;(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com