
实践探索题
(1)一个正方形的边长增加5cm,它的面积就增加35cm2,求这个正方形原来的边长.
(2)拼一拼,算一算:
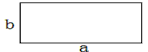
用4个长为a、宽为b的矩形拼成如图示的正方形,中间留下的“洞”恰好是一个小正方形,用不同方法计算中间小正方形的面积.你发现了什么?

|
解 (1)设这个正方形原来的边长为x cm,则新正方形的边长为(x+5)cm.据题意,得 (x+5)2-x2=35. 解这个方程,得 x2+10x+25-x2=35, 10x+25=35, 10x=10, 所以 x=1. 答:这个正方形原来的边长为1cm. (2)一方面,因为S小正方形=S大正方形-4S矩形,故 S小正方形=(a+b)2-4ab =a2+2ab+b2-4ab =a2-2ab+b2. 另一方面,由图可知小正方形的边长为(a-b),则由正方形面积公式,得 S小正方形=(a-b)2. 显然,可得出结论:(a-b)2=a2-2ab+b2. 分析 (1)题设未知数,据题意,列出方程,即可求解. (2)一方面,S小正方形=S大正方形-4S矩形;另一方面,由图可知小正方形的边长为(a-b). |


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:




查看答案和解析>>
科目:初中数学 来源: 题型:解答题




查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:《第3章 圆》2009年整章水平测试(解析版) 题型:解答题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com