




 )x-
)x- =0在[-1,3]上有且仅有一个解,则f(x)=x2-(2m+
=0在[-1,3]上有且仅有一个解,则f(x)=x2-(2m+ )x-
)x- ,可以得出:f(-1)×f(3)≤0,然后解关于m的不等式.
,可以得出:f(-1)×f(3)≤0,然后解关于m的不等式.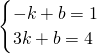 ,
,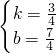
 x+
x+ ,
, x+
x+ 与y=x2-2mx+1在x=[-1,3]上有且仅有一个交点,
与y=x2-2mx+1在x=[-1,3]上有且仅有一个交点, x+
x+ =x2-2mx+1,
=x2-2mx+1, )x-
)x- =0在[-1,3]上有且仅有一个解,
=0在[-1,3]上有且仅有一个解, )x-
)x- ,可以得出:f(-1)×f(3)≤0
,可以得出:f(-1)×f(3)≤0 )-
)- ]≤0
]≤0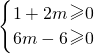 或
或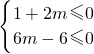 ,
, .
. 在这个范围内,
在这个范围内, )x-
)x- 在区间[-1,3]上的值域是解决此题的关键.
在区间[-1,3]上的值域是解决此题的关键. 

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知关于x 的一元二次方程(m+2)x2-2x-1=0.
已知关于x 的一元二次方程(m+2)x2-2x-1=0.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com