
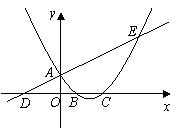
已知:直线![]() 与
与![]() 轴交于A,与
轴交于A,与![]() 轴交于D,抛物线
轴交于D,抛物线![]() 与直线交于A、E两点,与
与直线交于A、E两点,与![]() 轴交于B、C两点,且B点坐标为 (1,0).
轴交于B、C两点,且B点坐标为 (1,0).![]()
(1)求抛物线的解析式;
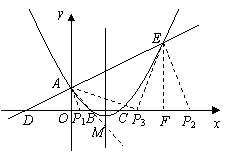
(2)动点P在![]() 轴上移动,当△PAE是直角三角形时,求点P的坐标.
轴上移动,当△PAE是直角三角形时,求点P的坐标.
(3)在抛物线的对称轴上找一点M,使![]() 的值最大,求出点M的坐标.
的值最大,求出点M的坐标.
解:(1)将A(0,1)、B(1,0)坐标代入![]() 得
得
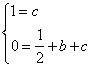 解得
解得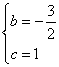
∴抛物线的解折式为![]() .
.
(2)设点E的横坐标为m,则它的纵坐标为![]()
则E(![]() ,
,![]() ).
).
又∵点E在直线![]() 上,
上,
∴![]() .
.
 解得
解得![]() (舍去),
(舍去),![]() .
.
∴E的坐标为(4,3).
(Ⅰ)当A为直角顶点时
过A作![]() 交
交![]() 轴于
轴于![]() 点,设
点,设![]() .
.
易知D点坐标为(![]() ,0).
,0).
由![]() 得
得
![]() 即
即![]() ,∴
,∴![]()
![]() .
.
∴![]() .
.
(Ⅱ)同理,当![]() 为直角顶点时,
为直角顶点时,![]() 点坐标为(
点坐标为(![]() ,0).)
,0).)
(Ⅲ)当P为直角顶点时,过E作![]() 轴于
轴于![]() ,设
,设![]() .
.
由![]() ,得
,得![]() .
.
![]() .
.
由![]() 得
得![]() .
.
解得![]() ,
,![]() .
.
∴此时的点![]() 的坐标为(1,0)或(3,0).
的坐标为(1,0)或(3,0).
综上所述,满足条件的点P的坐标为(![]() ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(![]() ,0)
,0)
(3)抛物线的对称轴为![]() .
.
∵B、C关于![]()
![]() 对称,
对称,
∴![]() .
.
要使![]() 最大,即是使
最大,即是使![]() 最大.
最大.
由三角形两边之差小于第三边得,当A、B、M在同一直线上时![]() 的值最大.
的值最大.
易知直线AB的解折式为![]() .
.
∴由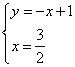 得
得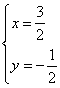 ∴M(
∴M(![]() ,-
,-![]() ).
).


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:2011-2012学年北京市西城区八年级上学期期末考试数学卷(带解析) 题型:解答题
已知:直线 与
与 轴交于点A,与
轴交于点A,与 轴交于点B.
轴交于点B.
【小题1】分别求出A,B两点的坐标;
【小题2】过A点作直线AP与 轴交于点P,且使OP=2OB,
轴交于点P,且使OP=2OB,
求△ABP的面积.
查看答案和解析>>
科目:初中数学 来源:2010年安徽省芜湖市初中毕业学业考试模拟试卷(一)数学卷 题型:解答题
(本小题满分12分)已知:直线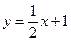 与
与 轴交于A,与
轴交于A,与 轴交于D,抛物线
轴交于D,抛物线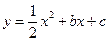 与直线交于A、E两点,与
与直线交于A、E两点,与 轴交于B、C两点,且B点坐标为 (1,0).
轴交于B、C两点,且B点坐标为 (1,0).
(1)求抛物线的解析式;
(2)动点P在 轴上移动,当△PAE是直角三角形时,求点P的坐标.
轴上移动,当△PAE是直角三角形时,求点P的坐标.
(3)在抛物线的对称轴上找一点M,使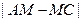 的值最大,求出点M的坐标.
的值最大,求出点M的坐标.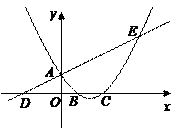
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市西城区八年级上学期期末考试(A卷)数学卷 题型:解答题
已知:直线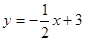 与
与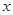 轴交于点A,与
轴交于点A,与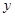 轴交于点B.
轴交于点B.
1.(1)分别求出A,B两点的坐标;
2.(2)过A点作直线AP与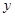 轴交于点P,且使OP=2OB,求△ABP的面积.
轴交于点P,且使OP=2OB,求△ABP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com