Question

△ABC的两条高线AD，BE所在直线交于H，若∠C=60°，则∠AHB的度数是

1. A.
   60°
2. B.
   30°或120°
3. C.
   120°
4. D.
   60°或120°

Answer 1

D
分析：根据AD、BE是△ABC的两条高，由此可以得到∠BEC=∠ADC=90°，根据四边形的内角和可以求出∠EHD的度数，然后根据对顶角相等即可求出∠AHB的度数．
解答：解：如图：∵∠C=60°，
而AD、BE是△ABC的两条高，
∴∠BEC=∠ADC=90°，
∴∠EHD=360°-90°-90°-60°=120°．
∴∠AHB=120°；
如图：∵BE与AD是高，
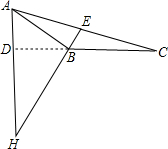
∴∠BEC=∠BDH=90°，
∵∠EBC=∠DBH，
∴∠AHB=∠C=60°．
∴∠AHB的度数是60°或120°．
故选D．
点评：本题主要考查了三角形的高的性质，也考查了三角形的内角和，还利用了对顶角相等等知识，题目难度不大．