
�Ķ����ϣ�
��1���������������� �Ĵ�С�Ƚϣ�������ķ�����
�Ĵ�С�Ƚϣ�������ķ�����
��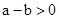 ʱ��һ����
ʱ��һ����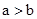 ��
��
�� ʱ��һ����
ʱ��һ���� ��
��
��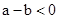 ʱ��һ����
ʱ��һ���� ��
��
������Ҳ��������ˣ����ǰ����ֱȽ���������С�ķ���������������
��2�����ڱȽ��������� �Ĵ�Сʱ�����ǻ����������ǵ�ƽ�����бȽϣ�
�Ĵ�Сʱ�����ǻ����������ǵ�ƽ�����бȽϣ�
��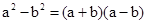 ��
��
�ࣨ ���루
���루 ���ķ�����ͬ
���ķ�����ͬ
�� ��0ʱ��
��0ʱ�� ��0����
��0����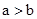
�� =0ʱ��
=0ʱ�� =0����
=0����
�� ��0ʱ��
��0ʱ�� ��0����
��0����
�������ʵ�����⣺
��1�������ϣ���ʦ��ͬѧ���������ּ����壬����ͬѧ����3��A4ֽ��7��B5ֽ������ͬѧ����2��A4ֽ��8��B5ֽ����ÿ��A4ֽ�����Ϊx��ÿ��B5ֽ�����Ϊy����x��y������ͬѧ����ֽ�����ΪW1������ͬѧ����ֽ�����ΪW2���ش��������⣺
��W1= ����x��y��ʽ�ӱ�ʾ��
W2= ����x��y��ʽ�ӱ�ʾ��
���������˭�õ�ֽ������
��2����ͼ1��ʾ��Ҫ��ȼ���ܵ�l����һ����վ���ֱ���A��B����������֪A��B��l�ľ���ֱ���3km��4km����AC=3km��BE=4km����AB=xkm����������ַ�����

����һ����ͼ2��ʾ��AP��l�ڵ�P����վ���ڵ�P�����÷����йܵ�����a1=AB+AP��
����������ͼ3��ʾ����A�����A����l�Գƣ�A��B��l�ཻ�ڵ�P����վ���ڵ�P�����÷����йܵ�����a2=AP+BP��
���ڷ���һ�У�a1= km���ú�x��ʽ�ӱ�ʾ����
���ڷ������У�a2= km���ú�x��ʽ�ӱ�ʾ����
���������Ҫʹ����������ܵ��϶̣�Ӧѡ��һ���Ƿ�������
��1����3x+7y��2x+8y������ͬѧ��ֽ���������2����x+3�� �۵�x��6.5ʱ��ѡ�����������ܵ��϶̣���x=6.5ʱ�����ַ���һ������0��x��6.5ʱ��ѡ��һ�������ܵ��϶�
�۵�x��6.5ʱ��ѡ�����������ܵ��϶̣���x=6.5ʱ�����ַ���һ������0��x��6.5ʱ��ѡ��һ�������ܵ��϶�
���������⣺��1����3x+7y��2x+8y��
��W1��W2=��3x+7y������2x+8y��=x��y��
��x��y����x��y��0����W1��W2��0��
��W1��W2����������ͬѧ��ֽ���������
��2����x+3��
�� ��
��
�ۡ�
�൱ ��0����a1��a2��0��a1��a2��ʱ��6x��39��0�����x��6.5��
��0����a1��a2��0��a1��a2��ʱ��6x��39��0�����x��6.5��
�� =0����a1��a2=0��a1=a2��ʱ��6x��39=0�����x=6.5��
=0����a1��a2=0��a1=a2��ʱ��6x��39=0�����x=6.5��
�� ��0����a1��a2��0��a1��a2��ʱ��6x��39��0�����x��6.5��
��0����a1��a2��0��a1��a2��ʱ��6x��39��0�����x��6.5��
������������x��6.5ʱ��ѡ�����������ܵ��϶̣�
��x=6.5ʱ�����ַ���һ����
��0��x��6.5ʱ��ѡ��һ�������ܵ��϶̡�
��1����W1=3x+7y��W2=2x+8y��
��2����a1=AB+AP=x+3��
�ڹ�B��BM��AC��M��
��AM=4��3=1��
�ڡ�ABM�У��ɹ��ɶ����ã�BM2=AB2��12=x2��1��
�ڡ�A��MB�У��ɹ��ɶ����ã�
AP+BP=A��B= ��
��
�۸����Ķ����ϵķ�����⡣


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 6 |
| 1 |
| 10 |
| 2 |
| 5 |
| 1 |
| 30 |
| 5 |
| 6 |
| 1 |
| 2 |
| 1 |
| 30 |
| 1 |
| 3 |
| 1 |
| 30 |
| 1 |
| 10 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 42 |
| 1 |
| 6 |
| 3 |
| 14 |
| 2 |
| 3 |
| 2 |
| 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
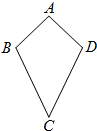 ������ʶ�ı��Σ�
������ʶ�ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
|
|
| (x2-x1)2+(y2-y1)2 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 10 |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
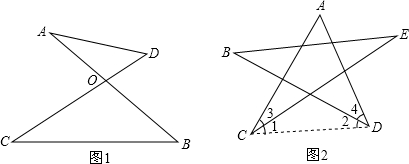
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com