
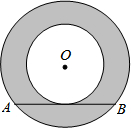
 如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是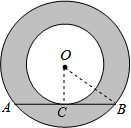 解:设AB与小圆切于点C,连结OC,OB.
解:设AB与小圆切于点C,连结OC,OB.| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 月均用水量x/m3 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | x>20 |
| 频数/户 | 12 | 20 | 3 | ||
| 频率 | 0.12 | 0.07 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、抛一枚硬币正面朝上的机会与抛一枚图钉钉尖着地的机会一样大 |
| B、为了了解泰州火车站某一天中通过的列车车辆数,可采用普查的方式进行 |
| C、彩票中奖的机会是1%,买100张一定会中奖 |
| D、泰州市某中学学生小亮,对他所在的住宅小区的家庭进行调查,发现拥有空调的家庭占65%,于是他得出泰州市拥有空调家庭的百分比为65%的结论 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com