
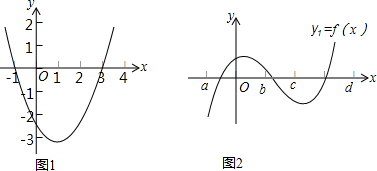
���� ��1���ٸ��ݺ����������ԣ�����ֵ�ij˻����ɵô𰸣�
�ڸ���ͼ����x��Ľ��㣬�ɵô𰸣�
��2���ٸ�����㺯��ֵ���ɵ÷��̣����ݽ�һԪ���η��̣��ɵô𰸣�
�ڽ�x1��x2�ı���ʽ����x1��1��x2�м������a��ȡֵ��Χ�����a�����������������a��ֵ���ɴ˿�ȷ�������ߵĽ���ʽ����PQ��ȡֵ��Χʱ����C��CD��x����D������CQ�����������ߵĽ���ʽ������õ�C�����꣬���ɵõ�AD��CD�ij����ɴ˿������BAC=60�㣬���������ߵĶԳ��Լ��ɵõ���ABC=��BAC=60�㣬�ɴ˿�֪��ABC�ǵȱ������Σ�����AMP����BNPҲ�ǵȱ������Σ���ôM��N�ֱ����߶�OC���߶�BC�ϣ���֪CM��PN��MP��BC�����ı���PNCM��ƽ���ı��Σ���Q��MN���е㣬��QҲ��CP���е㣬��C��Q��P���㹲�ߣ��ɴ˿ɵ�PC=2PQ���ڵȱ�������ABC�У�P���߶�AB���˶����Ҳ���A��B�غϣ����PQ��ȡֵ��ΧӦ����AD��AC��֮�䣬�ɾݴ����PQ��ȡֵ��Χ��
��� �⣺��1������ͼ��1����f��a��•f��b����0��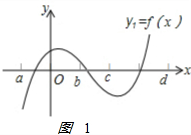
����a��x��b��Χ��y1=f��x�������ĸ����� 1��
�ʴ�Ϊ������1��
��2���١�x1��x2�����
�൱y=0ʱ����-$\sqrt{3}{x^2}-2\sqrt{3}��a-1��x-\sqrt{3}��{a^2}-2a��$=0��
���̿ɻ���Ϊ x2+2��a-1��x+��a2-2a��=0��
�ⷽ�̣���x=-a��x=-a+2��
��x1��1��x2��-a��-a+2��
��x1=-a��x2=-a+2��
�ڡ�x1��1��x2��
��-a��1��-a+2��
��-1��a��1��
��a��������
��a=0�����������ߵı���ʽΪy=-$\sqrt{3}$x2+2$\sqrt{3}$��
��ʱ����C������ΪC��1��$\sqrt{3}$����ͼ2��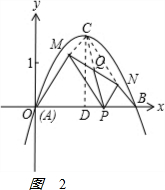 ��
��
��CD��AB��D������CQ��
��AD=1��CD=$\sqrt{3}$��tan��BAC=$\sqrt{3}$��
���BAC=60��
�ɒ����ߵĶԳ��Կ�֪��ABC�ǵȱ������Σ�
�ɡ�APM�͡�BPN�ǵȱ������Σ��߶�MN���е�ΪQ�ɵã�
��M��N�ֱ���AC��BC���ϣ��ı���PMCN��ƽ���ı��Σ�
C��Q��P���㹲�ߣ���PQ=$\frac{1}{2}$PC��
�ߵ�P�߶�AB���˶��Ĺ����У�P��A��B���㲻�غϣ�
DC��PC��AC��DC=$\sqrt{3}$��AC=2��
��$\frac{DC}{2}$��PQ��$\frac{AC}{2}$��
��$\frac{\sqrt{3}}{2}$��PQ��1��
�߶�PQ�ij���ȡֵ��ΧΪ��$\frac{{\sqrt{3}}}{2}$��PQ��1��
���� ���⿼���˶��κ����ۺ��⣬���κ�������ʽ��ȷ�����ȱ������ε����ʵ�֪ʶ���ۺ�Ӧ��������������ѵ�����PQ��ȡֵ��Χ���������ղ���������������ߡ��ȱ������Ρ�����ʽ�����֪ʶ�ǽ�����Ĺؼ���


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6ab-b=6a | B�� | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ | C�� | a8��a2=a4 | D�� | ��a2b��3=a6b3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
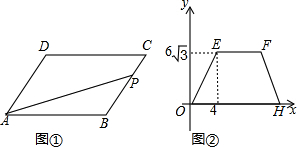
| A�� | 11 | B�� | 14 | C�� | 8+$\frac{3}{2}\sqrt{3}$ | D�� | 8+3$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
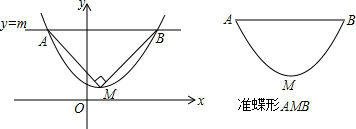
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
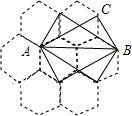 �䳲�Ĺ���dz���������ѧ����ͼ����7����״����С��ȫ��ͬ������������ɵķ������磬�������εĶ����Ϊ��㣬���һ�������ε��������㶼�ڸ���ϣ���֮Ϊ��������Σ���ͼ��ABΪб�ߵĸ��ֱ�������ι���4������ABC������֮һ�����ڷ䳲�������У����ABCȫ�ȵĸ�������Σ�������ABC������84��
�䳲�Ĺ���dz���������ѧ����ͼ����7����״����С��ȫ��ͬ������������ɵķ������磬�������εĶ����Ϊ��㣬���һ�������ε��������㶼�ڸ���ϣ���֮Ϊ��������Σ���ͼ��ABΪб�ߵĸ��ֱ�������ι���4������ABC������֮һ�����ڷ䳲�������У����ABCȫ�ȵĸ�������Σ�������ABC������84���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
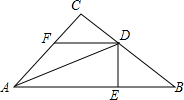 ��ͼ���ڡ�ABC�У���ACB=90�㣬ADƽ�֡�BAC��DE��AB��E��BD=DF����֤��BE=CF��
��ͼ���ڡ�ABC�У���ACB=90�㣬ADƽ�֡�BAC��DE��AB��E��BD=DF����֤��BE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
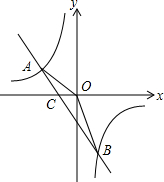 ��֪����������y=$\frac{{k}_{1}}{3x}$��ͼ����һ�κ���y=k2x+m��ͼ����A��-1��a����B��$\frac{1}{3}$��-3�����㣬����AO��
��֪����������y=$\frac{{k}_{1}}{3x}$��ͼ����һ�κ���y=k2x+m��ͼ����A��-1��a����B��$\frac{1}{3}$��-3�����㣬����AO���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
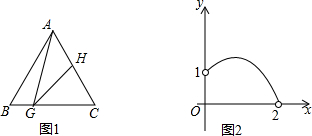 ��ͼ1���ڵȱ�������ABC�У�AB=2��G��BC����һ�������Ҳ����B��C�غϣ�H��AC����һ�㣬�ҡ�AGH=30�㣮��BG=x��ͼ��ij���߶γ�Ϊy��y��x����ĺ�����ϵ��ͼ�������ͼ2��ʾ���������߶ο�����ͼ�еģ�������
��ͼ1���ڵȱ�������ABC�У�AB=2��G��BC����һ�������Ҳ����B��C�غϣ�H��AC����һ�㣬�ҡ�AGH=30�㣮��BG=x��ͼ��ij���߶γ�Ϊy��y��x����ĺ�����ϵ��ͼ�������ͼ2��ʾ���������߶ο�����ͼ�еģ�������| A�� | �߶�CG | B�� | �߶�AG | C�� | �߶�AH | D�� | �߶�CH |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com