
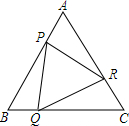
 如图所示.△ABC是边长为3的等边三角形,P,Q,R分别是AB,BC,CA上一动点,它们相同的速度,P由A向B运动,Q由B向C运动,R由C向A运动.
如图所示.△ABC是边长为3的等边三角形,P,Q,R分别是AB,BC,CA上一动点,它们相同的速度,P由A向B运动,Q由B向C运动,R由C向A运动.分析 (1)由等边三角形的性质可知∠A=∠B=∠C=60°,AB=BC=AC,由P,Q,R分别是AB,BC,CA上一动点,它们相同的速度,P由A向B运动,Q由B向C运动,R由C向A运动.可知AP=BQ=CR,BP=CQ=AR,从而可证得△BPQ≌△CQR≌△ARP,得到PQ=QC=RA即可;
(2)设AP=x,则AR=BP=3-x,△APR的边AP上的高为sin60°×AR,S△APR=$\frac{1}{2}×AP×sin60°×AR$,根据△PQR的面积为S=S△ABC-3S△APR,即可求出s与x之间函数关系式;
(3)把(2)中函数关系式变形为顶点式,根据二次函数的性质求出当x为何值时,s的最小值.
解答 解:(1)∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC,
∵P,Q,R分别是AB,BC,CA上一动点,它们相同的速度,P由A向B运动,Q由B向C运动,R由C向A运动,
∴AP=BQ=CR,BP=CQ=AR,
在△BPQ、△CQR和△ARP中,
$\left\{\begin{array}{l}{AP=BQ=CR}\\{∠A=∠B=∠C}\\{BP=CQ=AR}\end{array}\right.$,
∴△BPQ≌△CQR≌△ARP,
∴PQ=QC=RA,
∴△PQR是等边三角形;
(2)设AP=x,则AR=BP=3-x,
∴△APR的边AP上的高为sin60°×AR,
S△APR=$\frac{1}{2}×AP×sin60°×AR$
=$\frac{1}{2}$×x×$\frac{\sqrt{3}}{2}$×(3-x)
=-$\frac{\sqrt{3}}{4}$x2+$\frac{3\sqrt{3}}{4}$x,
∵△PQR的面积为S=S△ABC-3S△APR,
∴S=$\frac{1}{2}×3×\frac{3\sqrt{3}}{2}$-3(-$\frac{\sqrt{3}}{4}$x2+$\frac{3\sqrt{3}}{4}$x)
=$\frac{3\sqrt{3}}{4}$x2-$\frac{9\sqrt{3}}{4}$x+$\frac{9\sqrt{3}}{4}$;
(3)S=$\frac{3\sqrt{3}}{4}$x2-$\frac{9\sqrt{3}}{4}$x+$\frac{9\sqrt{3}}{4}$
=$\frac{3\sqrt{3}}{4}$(x-$\frac{3}{2}$)2+$\frac{9\sqrt{3}}{16}$
∴当x为$\frac{3}{2}$时,s有最小值,最小值是$\frac{9\sqrt{3}}{16}$.
点评 此题考查等边三角形的性质与判定以及二次函数的实际应用,利用特殊角的三角函数,以及等边三角形的性质求得底和高是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com