练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．如图，点E在?ABCD的边AD上，沿BE折叠，点A落在边CD上的点F处，若△FDE的周长为8，△FCB的周长为22．求FC的长．

    分析 根据翻转变换的性质得到EF=EA，BF=BA，根据平行四边形的性质得到AD=BC，AB=CD，根据三角形的周长公式计算即可．

    解答 解：由折叠的性质可知，EF=EA，BF=BA，
    ∵四边形ABCD是平行四边形，
    ∴AD=BC，AB=CD，
    由题意得，BF+BC+CF=22，
    则DC+BC+CF=22，
    DE+DF+EF=8，
    ∴DE+EA+DF=AD+DF=8，
    ∴（DC+BC+CF）-（AD+DF）=22-8=14，即2FC=14，
    解得，FC=7．

    点评 本题考查的是翻转变换的性质、平行四边形的性质，翻转变换是一种对称变换，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

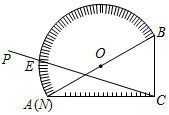    7．如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转，CP与量角器的半圆弧交于点E，第23秒时，点E在量角器上对应的度数是92度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．某商品进价为50元，若按标价的8折出售仍可获利20%，则按标价出售可获利25元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，正六边形ABCDEF内接于⊙O，连接AD、BD，则∠DAB的余弦值是$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．（1）已知x=-2是关于x的方程k-x-k（x+4）=-1的解，求k的值．
    （2）在（1）的条件下，已知线段AB=12cm，点C是直线AB上一点，且AC：BC=1：k，若点D是AC的中点，求线段BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．在正三角形、正四边形、正五边形、正六边形、正八边形5个图形中既是轴对称又是中心对称的图形有（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．在⊙O中，将圆心绕着圆周上一点A旋转一定角度θ，使旋转后的圆心落在⊙O上，则θ的值可以是（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．小明将两块都含45°的三角板按如图所示放置，小明用量角器测得∠AOD=150°，则∠COB的度数为30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．为进一步发展基础教育，近年来某县加大了对教育经费的投入，2014年投入3000万元，2016年投入7500万元，假设该县投入教育经费的年平均增长率为x，下面根据题意列出的方程正确的是（　　）
    A．3000x2=7500B．3000（1+x）2=7500
    C．3000（1+x%）2=7500D．3000（1+x）+3000（1+x）2=7500

    查看答案和解析>>

    同步练习册答案