
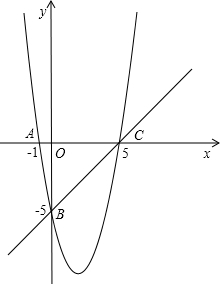
 -5)、C(5,0).
-5)、C(5,0).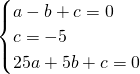 ,
, ,
,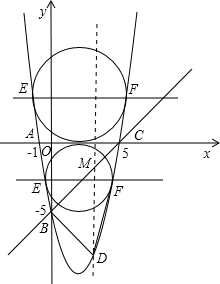 ①当直线EF在x轴上方时,设圆的半径为R(R>0),
①当直线EF在x轴上方时,设圆的半径为R(R>0),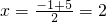
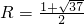 (
(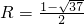 舍去);
舍去);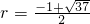 (
(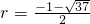 舍去),
舍去),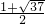 或
或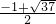 ,
,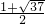 或
或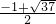 .
.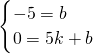 ,
,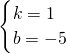
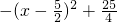
 时,DM有最大值为
时,DM有最大值为 ,
, ,
, )时,△BDC的面积最大=
)时,△BDC的面积最大=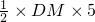
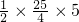
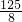 ,
, ,-
,-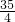 ),△BDC的面积是
),△BDC的面积是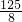 .
.

科目:初中数学 来源: 题型:
| 9 | x |
 交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.查看答案和解析>>
科目:初中数学 来源: 题型:
 5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )
5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )查看答案和解析>>
科目:初中数学 来源: 题型:
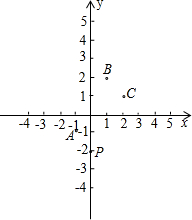 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为
如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
 BE.
BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com