
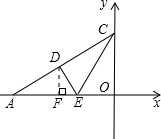
 如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC=
如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC=| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |


科目:初中数学 来源: 题型:
| 3 |
| 3 |
 在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
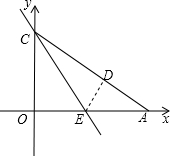 A在x轴上,点C在y轴上,OC=
A在x轴上,点C在y轴上,OC=| 3 |
查看答案和解析>>
科目:初中数学 来源:2010年浙江省舟山市初中毕业生学业水平考试调研试卷(解析版) 题型:解答题
 ,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
查看答案和解析>>
科目:初中数学 来源:2005年辽宁省沈阳市中考数学试卷(课标卷)(解析版) 题型:解答题
 ,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com