
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E. 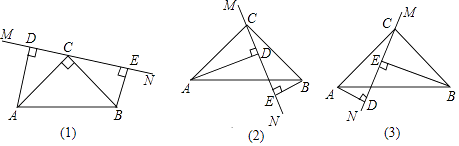
(1)当直线MN绕点C旋转到图(1)的位置时, 求证:①△ADC≌△CEB.②DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE之间的等量关系.
【答案】
(1)解:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠ACB=90°=∠CEB,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
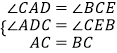 ,
,
∴△ADC≌△CEB(AAS);
②∵△ADC≌△CEB,
∴CE=AD,CD=BE,
∴DE=CE+CD=AD+BE
(2)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
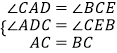 ,
,
∴△ADC≌△CEB(AAS);
∴CE=AD,CD=BE,
∴DE=CE﹣CD=AD﹣BE
(3)解:当MN旋转到题图(3)的位置时,AD,DE,BE所满足的等量关系是:DE=BE﹣AD.
理由如下:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
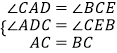 ,
,
∴△ADC≌△CEB(AAS),
∴CE=AD,CD=BE,
∴DE=CD﹣CE=BE﹣AD
【解析】(1)①根据AD⊥MN,BE⊥MN,∠ACB=90°,得出∠CAD=∠BCE,再根据AAS即可判定△ADC≌△CEB;②根据全等三角形的对应边相等,即可得出CE=AD,CD=BE,进而得到DE=CE+CD=AD+BE;(2)先根据AD⊥MN,BE⊥MN,得到∠ADC=∠CEB=∠ACB=90°,进而得出∠CAD=∠BCE,再根据AAS即可判定△ADC≌△CEB,进而得到CE=AD,CD=BE,最后得出DE=CE﹣CD=AD﹣BE;(3)运用(2)中的方法即可得出DE,AD,BE之间的等量关系是:DE=BE﹣AD.


科目:初中数学 来源: 题型:
【题目】如图,有一个立方体,它的表面涂满了红色,在它每个面上切两刀,得到27个小立方体,而且凡是切面都是白色.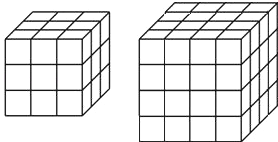
问:
(1)小立方体中三面红的有几块?两面红的呢?一面红的呢?没有红色的面呢?
(2)如果每面切三刀,情况又怎样呢?
(3)每面切n刀呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初中学生在家做家务情况,随机抽取了该校部分初中生进行调查,依据相关数据绘制成以下不完整的统计图.
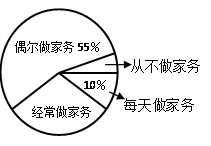
根据以上信息解答下列问题:
(1)此次调查该校抽取的初中生人数名,“从不做家务”部分对应的扇形的圆心角度数为;
(2)补全条形统计图;
(3)请估计该校2000名初中生中“经常做家务”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车. (注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)若到2020年该市政府将再建造 ![]() 个新公共自行车站点和配置
个新公共自行车站点和配置 ![]() 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?
辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
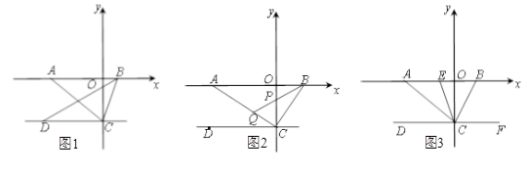
【题目】如图1,在平面直角坐标系中,点 ![]() 为
为 ![]() 轴负半轴上一点,点
轴负半轴上一点,点 ![]() 为
为 ![]() 轴正半轴上一点,
轴正半轴上一点, ![]() ,
, ![]() ,其中
,其中 ![]() ,
, ![]() 满足关系式:
满足关系式: ![]() +
+ ![]() .
.
(1)![]() = ,
= , ![]() = , △
= , △ ![]() 的面积为;
的面积为;![]()
(2)如图2,若 ![]() ⊥
⊥ ![]() ,点
,点 ![]() 线段
线段 ![]() 上一点,连接
上一点,连接 ![]() ,延长
,延长 ![]() 交
交 ![]() 于点
于点 ![]() ,当∠
,当∠ ![]() =∠
=∠ ![]() 时,求证:
时,求证: ![]() 平分∠
平分∠ ![]() ;
;
(3)如图3,若 ![]() ⊥
⊥ ![]() ,点
,点 ![]() 是点
是点 ![]() 与点
与点 ![]() 之间一动点,连接
之间一动点,连接 ![]() ,
, ![]() 始终平分∠
始终平分∠ ![]() ,当点
,当点 ![]() 在点
在点 ![]() 与点
与点 ![]() 之间运动时,
之间运动时, ![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣3x2先向右平移4个单位,再向下平移5个单位,所得图象的解析式为( )
A. y=﹣3(x﹣4)2﹣5B. y=﹣3(x+4)2+5
C. y=﹣3(x﹣4)2+5D. y=﹣3(x﹣4)2﹣5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com