练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    现有若干张边长为a的正方形A型纸片，边长为b的正方形B型纸片，长宽为a、b的长方形C型纸片，小明同学选取了4张A型纸片，9张B型纸片，12张C型纸片拼成了一个四边形，则此四边形的周长为
    8a+12b
    8a+12b
    ．（用a、b代数式表示）
    分析：根据题意表示出四边形的面积，开方求出边长，即可表示出周长．
    解答：解：根据题意得：4a2+12ab+9b2=（2a+3b）2，
    所拼成的四边形是个边长为（2a+3b）的正方形，其周长为8a+12b．
    故答案为：8a+12b．
    点评：此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，现有边长为a，边长为b的正方形卡片，和长为a，宽为b的长方形卡片各若干张．
    （1）用给出的卡片拼成一个长为2a+b．宽为a+2b的长方形，画出拼成后的图形并计算：（2a+b）（a+2b）
    （2）用上述卡片拼成一个面积为2a2+3ab+b2的长方形，画出拼成后的图形，并尝试对多项式2a2+3ab+b2进行分解因式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

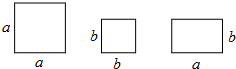
    很多代数原理都可以用几何模型解释．现有若干张如图所示的卡片，请拼成一个边长为（2a+b）的正方形（要求画出简单的示意图），并指出每种卡片分别用了多少张？然后用相应的公式进行验证．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

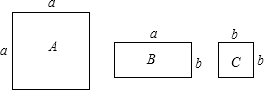    如图，有A、B、C三种不同型号的卡片，其中A型卡片是边长为a的正方形，B型卡片是长为b的长方形，C型卡片是边长为b的正方形，其中a＞b．现有A型卡片3张，B型卡片4张，C型卡片5张，从其中取出若干张，每种卡片至少取一张，把取出的这些卡片拼成一个正方形（所拼的图中既不能有缝隙，也不能有重合部分），所拼成的正方形的边长为
    a+b
    a+b
    ．

    查看答案和解析>>

    科目：初中数学 来源：学习周报　数学　华师大八年级版　2009－2010学年　第17期　总第173期 华师大版 题型：022

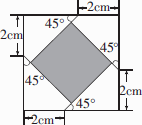
    现有若干张边长不相等但都大于4 cm的正方形纸片，从中任选一张，如图从距离正方形的四个顶点2 cm处，沿45°角画线，将正方形纸片分成5部分，则中间阴影部分的面积为________cm2；若从上述正方形纸片中再任选一张重复上述过程，并计算其阴影部分的面积，你能发现什么规律？________．

    查看答案和解析>>

    同步练习册答案