
分析 (1)延长AD至H,使HD=AD,连接CH,证得△ADB≌△HDC和△AHC≌△FEA,最后得出∠ACH+∠CHD+∠CAD=180°,进一步得出结论即可;
(2)由(1)△AHC≌△FEA,证得△AEG≌△BAD,得出△ABE是等边三角形,进一步证得△ACD≌△FAG利用在四边形ABCF中,∠ABC+∠BCF+∠CFA+∠BAF=360°,得出∠BCF=150°,证得∠BCM=30°,∠BMC=90°,求得结论BC=2BM.
解答 (1)证明:如图,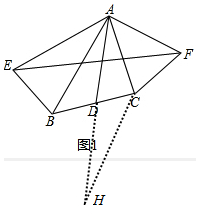
延长AD至H,使HD=AD,连接CH,
∵BD=CD,AD=HD,∠ADB=∠HDC
∴△ADB≌△HDC,
∴∠BAD=∠CHD,AB=HC,
∴∠BAC=∠BAD+∠CAD=∠CHD+∠CAD,
∵EF=2AD,HA=2AD,
∴EF=HA,
∵AE=AB,AB=HC,
∴HC=AE,
又AC=AF
∴△AHC≌△FEA,
∴∠EAF=∠ACH
∵∠ACH+∠CHD+∠CAD=180°
∴∠EAF+∠BAC=180°.
(2)BC=2BM.
证明:由(1)得∠AEG=∠BAD,
由(1)得,AD=$\frac{1}{2}$EF,又点G为EF中点,
∴EG=AD,
在△EAG和△ABD中,
$\left\{\begin{array}{l}{AE=AB}\\{∠AEG=∠BAD}\\{EG=AD}\end{array}\right.$,
∴△EAG≌△ABD,
∴∠EAG=∠ABC=60°,
∴△AEB是等边三角形,
∴∠ABE=60°,
∴∠CBM=60°,
在△ACD和△FAG中,
$\left\{\begin{array}{l}{AD=FG}\\{AG=CD}\\{AF=AC}\end{array}\right.$,
∴△ACD≌△FAG,
∴∠ACD=∠FAG,∠DAC=∠F,∠ADC=∠FGA,
∵AC=AF,
∴∠ACF=∠AFC,
在四边形ABCF中,∠ABC+∠BCF+∠CFA+∠BAF=360°,
则∠BCF=150°,
∴∠BCM=30°,
∴∠BMC=90°,
则BC=2BM.
点评 本题考查全等三角形的判定和性质,含30°角的直角三角形的性质,等腰三角形的判定与性质,掌握它们的判定定理和性质定理以及直角三角形的性质是解题的关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
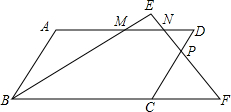 如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值.
如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
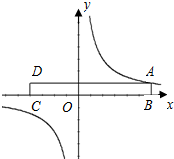 如图,将一张长方形的纸片ABCD沿x轴摆放,顶点A(6,1)恰好落在某双曲线上.现在AD边上找一点E,使得将纸片的右半部分沿OE所在直线折叠后,点A恰好还落在此双曲线上,则满足条件的点E的坐标为(1,1)(-1,1).
如图,将一张长方形的纸片ABCD沿x轴摆放,顶点A(6,1)恰好落在某双曲线上.现在AD边上找一点E,使得将纸片的右半部分沿OE所在直线折叠后,点A恰好还落在此双曲线上,则满足条件的点E的坐标为(1,1)(-1,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com