
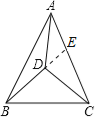
【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )

A. 100° B. 80° C. 70° D. 50°
【答案】A
【解析】试题分析:如果延长BD交AC于E,由三角形的一个外角等于与它不相邻的两个内角的和,得∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,所以∠BDC=∠ABE+∠BAE+∠ECD,又DA=DB=DC,根据等腰三角形等边对等角的性质得出∠ABE=∠DAB=20°,∠ECD=∠DAC=30°,进而得出结果.
解:延长BD交AC于E.
∵DA=DB=DC,
∴∠ABE=∠DAB=20°,∠ECD=∠DAC=30°.
又∵∠BAE=∠BAD+∠DAC=50°,
∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,
∴∠BDC=∠ABE+∠BAE+∠ECD=20°+50°+30°=100°.
故选A.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,有下列说法:
①点A与点B的距离是线段AB的长;
②点A到直线CD的距离是线段AD的长;
③线段CD是△ABC边AB上的高;
④线段CD是△BCD边BD上的高.
上述说法中,正确的个数为_________个

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将三张质地相同并分别标有数字1、2、3的卡片,背面朝上放在桌面上,洗匀后,甲同学从中随机抽取一张卡片.
(1)甲同学抽到卡片上的数恰好是方程x2﹣4x+3=0的根的概率为 ;
(2)甲乙两人约定:甲先随机抽取一张卡片后,背面朝上放回桌面洗匀,然后乙再随机抽取一张卡片,若两人所抽取卡片上的数字恰好是方程x2﹣4x+3=0的两个根,则甲获胜;否则乙获胜.请你通过列表或画树状图的方法,说明这个游戏是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
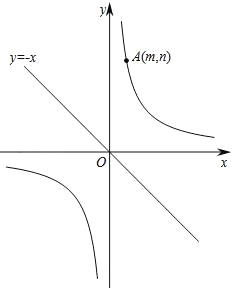
【题目】如图,已知直线y=﹣x和双曲线![]() (k>0),点A(m,n)(m>0)在双曲线
(k>0),点A(m,n)(m>0)在双曲线![]() 上.
上.
(1)当m=n=2时,
①直接写出k的值;
②将直线y=﹣x作怎样的平移能使平移后的直线与双曲线![]() 只有一个交点.
只有一个交点.
(2)将直线y=﹣x绕着原点O旋转,设旋转后的直线与双曲线![]() 交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:
交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:![]() 与
与![]() 的值存在怎样的数量关系?请说明理由.
的值存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小睿每天起床后必须要做的事情有穿衣(2分钟)、整理床(2分钟)、洗脸梳头(4分钟)、上厕所(5分钟)、烧饭(15分钟)、吃早饭(10分钟),完成这些工作共需38分钟,你认为最合理的安排应是 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com