
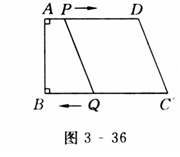
如图3-36所示,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24 ㎝,BC=26㎝,动点P从点A开始沿AD边以每秒1㎝的速度向D点运动,动点Q从点C开始沿CB边以每秒3㎝的速度向B运动,P,Q分别从A,C同时出发,当其中一点到达端点时,另一点也随 之停止运动,设运动时间为t s.
之停止运动,设运动时间为t s.
(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?
(3)t为何值时,四边形ABQP为矩形?
提示:本题的解法充分地体现了方程思想在几何中的应用,同时也体现了数形结合思想.解:由已知得AP=t,CQ=3t,PD=24-t,BQ=26-3t.(1)∵PD∥CQ,∴当PD=CQ时,即3t=24-t时,四边形PQCD为平行四边形,解得t=6.故当t=6时,四边形PQCD为平行四边形. (2)如图3—38所示,作DE⊥BC,PF⊥BC,垂足分别为E,F,则CE=2.当QF=CE时,即QF+CE=2CE=4时,四边形PQCD是等腰梯形.此时有CQ-EF=4,即3t—(24一t)=4,解得t=7.故当t=7时,四边形PQCD为等腰梯形.(3)若四边形ABQP为矩形,则AP=BQ,即t=26—3t,解得t=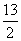 .故当t=
.故当t=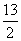 时,四边形ABQP为矩形.
时,四边形ABQP为矩形.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
在Rt△ABC中,AB=BC,∠B=90°,将一块等腰直角三角板的直角顶点O放在斜边AC
上,将三角板绕点O旋转.
(1)当点O为AC中点时:
①如图1,三角板的两直角边分别交AB,BC于E、F两点,连接EF,猜想线段AE、CF
与EF之间存在的等量关系(无需证明);
②如图2,三角板的两直角边分别交AB,BC延长线于E、F两点,连接E F,判断①中的
F,判断①中的
结论是否成立.若成立,请证明;若不成立,请说明理由;
(2)当点O不是AC中点时,如图3,三角板的两直角边分别交AB,BC于E、F两点,
若 ,则
,则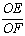 = .
= .
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,且AE=AD,BC=3AE, 则∠BAD等于 ( )
A.120° B.135° C.130°D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
下列条件中不能确定四边形ABCD是平行四边形的是( )
A.AB=CD,AD∥BC B.AB=CD,AB∥CD
C.AB∥CD,AD∥BC D.AB=CD,AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com