
 小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.
小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.分析 (1)列表得出所有等可能的情况数,找出甲乙在同一个楼层的情况数,即可求出所求的概率;
(2)分别求出两人获胜的概率比较得到公平与否,修改规则即可.
解答 解:(1)列表如下:
甲 乙 | 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | (3,2) | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
点评 此题考查了游戏公平性,以及列表法与树状图法,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.


科目:初中数学 来源: 题型:解答题
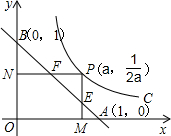 如图,已知动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM丄x轴于点M,PN丄y轴于点N,线段PM、PN分别与直线AB:y=-x+1交于点E,F,求AF•BE的值.
如图,已知动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM丄x轴于点M,PN丄y轴于点N,线段PM、PN分别与直线AB:y=-x+1交于点E,F,求AF•BE的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com