
分析 (1)a=1,b=3,按规则操作三次,第一次:c=7;第二次c=31;第三次c=255;
(2)p>q>0 第一次得:c1=pq+p+q=(q+1)(p+1)-1;第二次得:c2=(p+1)2(q+1)-1;所得新数大于任意旧数,故经过6次扩充,所得数为:(q+1)8(p+1)13-1,故可得结论.
解答 解:(1)a=1,b=3,按规则操作三次,
第一次:c=ab+a+b=1×3+1+3=7;
第二次,7>3>1所以有:c=3×7+3+7=31;
第三次:31>7>3所以有:c=7×31+7+31=255;
(2)p>q>0 第一次得:c1=pq+p+q=(q+1)(p+1)-1;
因为c>p>q,所以第二次得:c2=(c1+1)(p+1)-1=(pq+p+q)p+p+(pq+p+q)=(p+1)2(q+1)-1;
所得新数大于任意旧数,所以第三次可得c3=(c2+1)(c1+1)-1=(p+1)3(q+1)2-1
第四次可得:c4=(c3+1)(c2-1)-1=(p+1)5(q+1)3-1;
第五次可得:c5=(p+1)8(q+1)5-1;
故经过6次扩充,所得数为:(q+1)8(p+1)13-1
∴m=8,n=13,
∴m+n=21.
故答案为:255;21.
点评 本题考查了推理与论证以及新定义运算,考查学生分析解决问题的能力,求出经过6次操作后扩充所得的数是关键.


科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2-($\sqrt{5}$-$\sqrt{3}$)x-$\sqrt{15}$=0的一根,求?ABCD的周长.
如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2-($\sqrt{5}$-$\sqrt{3}$)x-$\sqrt{15}$=0的一根,求?ABCD的周长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
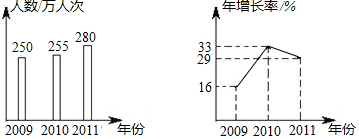
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com