
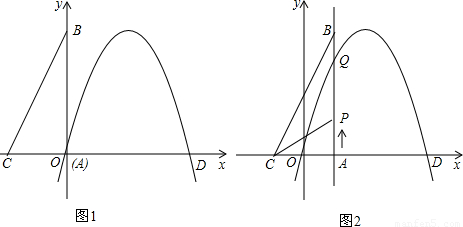
 x+d,得出
x+d,得出 x+d=-x2+4x整理后方程为:x2-
x+d=-x2+4x整理后方程为:x2- x+d=0此时方程有两个相等的实数根,
x+d=0此时方程有两个相等的实数根,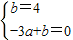 ,
,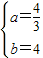 ,
, x+4;
x+4; x+4;
x+4; PQ•AC
PQ•AC ×3×(-t2+3t)
×3×(-t2+3t) (t2-3t)
(t2-3t) (t-
(t- )2+
)2+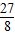
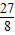 .
. x+d,
x+d, x+d=-x2+4x整理后方程为:x2-
x+d=-x2+4x整理后方程为:x2- x+d=0此时方程有两个相等的实数根,
x+d=0此时方程有两个相等的实数根,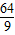 -4×1×d=0,
-4×1×d=0,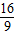 ,
, x+
x+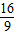 ,
, ,
, ,0)移动了
,0)移动了 个单位长度,
个单位长度, .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.查看答案和解析>>
科目:初中数学 来源: 题型:
 探照灯、锅盖天线、汽车灯等都利用了抛物线的一个原理:由它的焦点处发出的光线被反射后将会被平行射出.如图,由焦点O处发出的光线OB,OC经反射后沿与POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,则∠BOC=
探照灯、锅盖天线、汽车灯等都利用了抛物线的一个原理:由它的焦点处发出的光线被反射后将会被平行射出.如图,由焦点O处发出的光线OB,OC经反射后沿与POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,则∠BOC=查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0, ),点M是抛物线C2:
),点M是抛物线C2: (
( <0)的顶点.
<0)的顶点.

(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2012年湖北省鄂州市梁子湖区中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com