
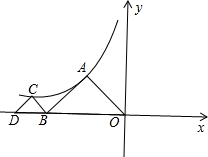
 如图:两个等腰直角三角形的两个直角顶点A、C都在y=
如图:两个等腰直角三角形的两个直角顶点A、C都在y= 上,若D(-8,0),则k=________.
上,若D(-8,0),则k=________.科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| GN+GC |
| NQ |
| GN-GC |
| NQ |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,有两个边长为2的正方形,将其中一个正方形沿对角线剪开成两个全等的等腰直角三角形,用这三个图片分别在网格备用图的基础上(只要再补出两个等腰直角三角形即可),分别拼符合要求的图形:(如图1)
 ????????????????????
???????????????????? 
图1??????????????????????????????????????? 图2
既不是轴对称图形,又不是中心对称图形?????????????? 是轴对称图形,不是中心对称图形
 ????????????????????
???????????????????? 
????????????????? 图3????????????????????????????????????? 图4
???????????? 是中心对称图形,不是轴对称图形?? ????? 既是轴对称图形,又是中心对称图形
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江西卷)数学(解析版) 题型:解答题
如图,有两个边长为2的正方形,将其中一个正方形沿对角线剪开成两个全等的等腰直角三角形,用这三个图片分别在网格备用图的基础上(只要再补出两个等腰直角三角形即可),分别拼出一个三角形、一个四边形、一个五边形、一个六边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com