
 如图,AB,AC是内接于⊙O的两条弦,M、N分别为
如图,AB,AC是内接于⊙O的两条弦,M、N分别为 ,
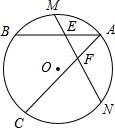
, 的中点,MN分别交AB,AC于E,F.判断三角形AEF的形状并给予证明.
的中点,MN分别交AB,AC于E,F.判断三角形AEF的形状并给予证明. 解:△AEF是等腰三角形.
解:△AEF是等腰三角形. ,
, 的中点,
的中点, ,
, 的中点,根据垂径定理的即可求得OM⊥AB,ON⊥BC,由等腰三角形的性质,可得∠M=∠N,继而可证得∠AEF=∠AFE,则可证得△AEF是等腰三角形.
的中点,根据垂径定理的即可求得OM⊥AB,ON⊥BC,由等腰三角形的性质,可得∠M=∠N,继而可证得∠AEF=∠AFE,则可证得△AEF是等腰三角形.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:模拟题 题型:探究题
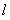 同旁的两个定点.
同旁的两个定点. 上确定一点P,使
上确定一点P,使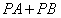 的值最小.
的值最小.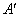 ,连结
,连结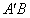 交l点P,则
交l点P,则 的值最小(不必证明)。
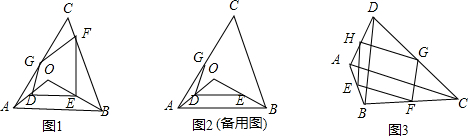
的值最小(不必证明)。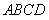 的边长为2,E为的AB中点,P是AC上一动点.连结
的边长为2,E为的AB中点,P是AC上一动点.连结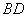 ,由正方形对称性可知,B与D关于直线
,由正方形对称性可知,B与D关于直线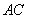 对称.连结
对称.连结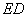 交AC于P,则
交AC于P,则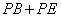 的最小值是_____ ;
的最小值是_____ ;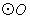 的半径为2,点
的半径为2,点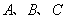 在
在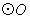 上,
上,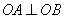 ,
,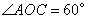 ,P是OB上一动点,求
,P是OB上一动点,求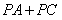 的最小值;
的最小值;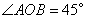 ,P是
,P是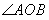 内一点,
内一点,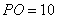 ,
,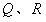 分别是
分别是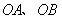 上的动点,求
上的动点,求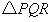 周长的最小值。
周长的最小值。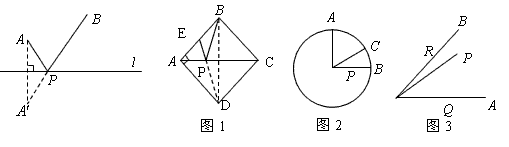
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com