试题分析:
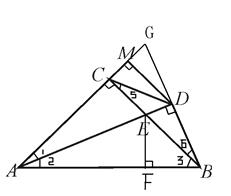
①过点E作EF⊥AB于点F。已知Rt△ABC中,AC=BC∴∠3=45°。
∵在△ACE和△AFE中,∠ACB=90°∴∠EFA=∠ACB=90°,且AE平分∠BAC,所以∠1=∠2.且AE=AE。所以△ACE≌△AFE。∴CE=EF,AC=AF。在Rt△EFB中,∠3=45°,所以EF=FB。所以BC+CE="=AF+FB=AB" 。
②作 AM与BD延长线相交于G,在Rt△ADG和Rt△BCG中,∠G= ∠G,∠GCB= ∠GDA=90°。
∴∠1= ∠6,已知: AC=BC
∴ Rt△GBC≡Rt△EAC,∴BG="AE" 。又∵DG=DB(可通过角边角证明Rt△ADG≌Rt△ADB)
∴ BD=
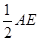
③BD=CD:证明:∵由②知DG=DB∴在Rt△BGC中,CD为斜边中线。∴CD=
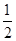
BG=BD
④∵BD=CD所以∠5=∠6=∠1,∵BC∥MD,∴∠MDC=∠5,∠GDM=∠6,∴∠GDC=45°。
∵∠GDA=90°,∴∠ADC=45°
⑤由上可得 AB=AG=AC+CG
∵ DM⊥AC 即 DM//BC, 又 DG=DB
∴ MC=MG=
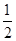
CG
∴ AB-BC=CG=2MC
点评:本题难度较高。学生需要通过辅助线补充好全等直角三角形等条件来证明。一般选择题中出现这种证明过程较复杂的题目,可以直接用排除法排除。

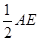 ,③BD=CD,④∠ADC=45°,⑤AC+AB=2AM;其中不正确的结论有( )
,③BD=CD,④∠ADC=45°,⑤AC+AB=2AM;其中不正确的结论有( )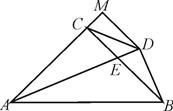

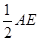
 BG=BD
BG=BD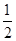 CG
CG

 ,且DE交△ABC外角
,且DE交△ABC外角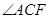 的平分线CE于点E,求证:AD=DE.
的平分线CE于点E,求证:AD=DE.
