
已知:二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() 对称轴是直线
对称轴是直线![]() 且图象向右平移一个单位后经过坐标原点
且图象向右平移一个单位后经过坐标原点![]()
(1)求这个二次函数的解析式;
(2)直线![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() 为抛物线顶点.若
为抛物线顶点.若![]() 求
求![]() 的值.
的值.
(3)在(2)问的前提下,![]() 为抛物线对称轴上一点,且满足
为抛物线对称轴上一点,且满足![]() 在
在![]() 轴右侧的抛物线上是否存在点
轴右侧的抛物线上是否存在点![]() 使得
使得![]() 的面积等于
的面积等于![]() 若存在,求出点
若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
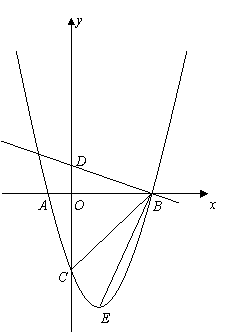 |
解:(1)由题意,![]()
![]() 对称轴是直线
对称轴是直线![]()
∴![]() ……………………………………………………………………1分
……………………………………………………………………1分
把![]() ,
,![]() 分别代入
分别代入![]() 得
得![]() ……………2分
……………2分
解得![]()
∴这个二次函数的解析式为![]() ………………………………3分
………………………………3分
(2)![]() 直线
直线![]() 与
与![]() 轴交于
轴交于![]() ,∴
,∴![]()
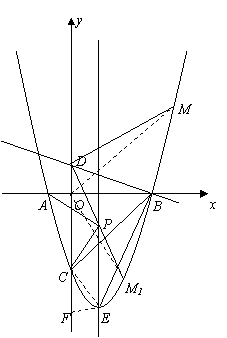 由
由![]() 得
得![]()
连接![]() 过
过![]() 作
作![]() 轴于
轴于![]() (如图1),则
(如图1),则![]()
![]() 抛物线
抛物线![]() 与
与![]() 轴交于
轴交于![]()
∴![]()
∴![]()
![]() ,
,
![]()
∴![]()
![]()
![]() [来源:Zxxk.Com]
[来源:Zxxk.Com]
∴![]()
∴![]() ……
……
∴![]()
∴![]()
(3)设![]()
` ![]()
∴![]() 即
即![]()
解得![]()
∴![]()
∴![]() ………………………………8分
………………………………8分
法一:设存在符合条件的点![]() 则
则![]()
①当![]() 在直线
在直线![]() 上侧时,连接
上侧时,连接![]() (如图1),
(如图1),
则![]()
即![]()
![]()
整理,得![]()
解得![]() (舍去),
(舍去),![]()
把![]() 代入
代入![]() 得
得![]()
∴![]() ……………………………………10分
……………………………………10分
②当![]() 在直线
在直线![]() 下侧时,不妨叫
下侧时,不妨叫![]() 连接
连接![]() (如图1),
(如图1),
则![]()
即![]()
![]()
整理,得![]()
解得![]() (舍去)
(舍去)
把![]() 代入
代入![]() 得
得![]()
∴![]()
综上所述,存在符合条件的点![]() 其坐标为
其坐标为![]() 或
或![]() .
.
………………………………………………………………12![]() 分
分
法二:设存在符合条件的点![]() 则
则![]()
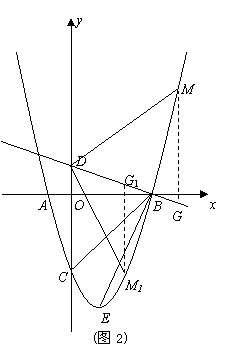 ①当
①当![]() 在直线
在直线![]() 上侧时,过
上侧时,过![]() 作
作![]() 轴,
轴,
交![]() 于
于![]() (如图2)
(如图2)
设![]() 到
到![]() 距离分别为
距离分别为![]() 则
则
![]()
即![]()
![]()
![]()
整理,得![]()
解得![]() (舍去),
(舍去),![]()
把![]() 代入
代入![]() 得
得![]()
∴![]() ……………………………………10分
……………………………………10分
②当![]() 在直线
在直线![]() 下侧时,不妨叫
下侧时,不妨叫![]() 过
过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() (如图2)
(如图2)
设![]() 到
到![]() 距离分别为
距离分别为![]() 则
则![]()
即![]()
![]()
![]()
整理,得![]()
解得![]() (舍去)
(舍去)
把![]() 代入
代入![]() 得
得![]()
∴![]()
综上所述,存在符合条件的点![]() 其坐标为
其坐标为![]() 或
或![]() .…………12分
.…………12分
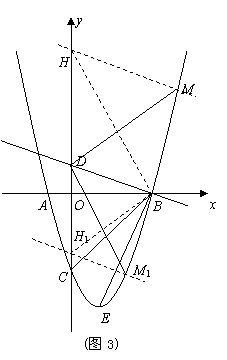 法三:①当
法三:①当![]() 在直线
在直线![]() 上侧时,过
上侧时,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() 连接
连接![]() (如图3)
(如图3)
则![]() ,即
,即![]()
![]() ∴
∴![]()
∴![]()
∴直线![]() 解析式为
解析式为![]()
联立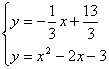 得
得![]() 或
或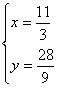
![]()
![]() 在
在![]() 轴右侧, ∴
轴右侧, ∴![]() 坐标为
坐标为![]()
…………………………………………10分
②当![]() 在直线
在直线![]() 下侧时,不妨叫
下侧时,不妨叫![]() 过
过![]() 作
作![]() ,交
,交![]() 轴于
轴于![]()
连接![]() (如图3),同理可得
(如图3),同理可得![]()
∴![]()
∴直线![]() 解析式为
解析式为![]()
联立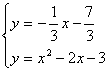 得
得![]() 或
或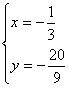
![]()
![]() 在
在![]() 轴右侧,∴
轴右侧,∴![]() 坐标为
坐标为![]()
综上所述,存在符合条件的点![]() 其坐标为
其坐标为![]() 或
或![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com