
 Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线$y=\frac{k}{x}(k≠0)$经过CD点及AB的中点D,S△BCD=4,则k的值为( )
Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线$y=\frac{k}{x}(k≠0)$经过CD点及AB的中点D,S△BCD=4,则k的值为( )| A. | 8 | B. | -8 | C. | -10 | D. | 10 |
分析 OA=a,AE=b,则C点坐标(a,$\frac{k}{a}$),B点坐标(b,$\frac{k}{a}$ ),根据S△BCD=S△ACD=4,得出S△ACB=10=$\frac{1}{2}$AC•BC=$\frac{1}{2}$•(-$\frac{k}{a}$)b得出bk=-20a①,先求得D的坐标,根据点D在双曲线上,得出($\frac{1}{2}$b+a)($\frac{1}{2}$•$\frac{k}{a}$)=k,则b=2a②,结合①②,即可求得k的值.
解答 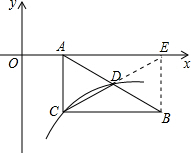 解:设OA=a,AE=b,则C点坐标(a,$\frac{k}{a}$),B点坐标(a+b,$\frac{k}{a}$ )
解:设OA=a,AE=b,则C点坐标(a,$\frac{k}{a}$),B点坐标(a+b,$\frac{k}{a}$ )
∵AD=BD,
∴S△BCD=S△ACD=4,
∴S△ACB=8=$\frac{1}{2}$AC•BC=$\frac{1}{2}$•(-$\frac{k}{a}$)•b
得bk=-16a,
∵B点坐标(a+b,$\frac{k}{a}$ )
∴点D在抛物线上,D点坐标($\frac{1}{2}$b+a,$\frac{1}{2}$•$\frac{k}{a}$)
则($\frac{1}{2}$b+a)($\frac{1}{2}$•$\frac{k}{a}$)=k,
则b=2a,
解$\left\{\begin{array}{l}{bk=-16a}\\{b=2a}\end{array}\right.$,
得k=-8.
故选B.
点评 本题考查了反比例函数系数k的几何意义:三角形的面积等于$\frac{1}{2}$|k|.


科目:初中数学 来源: 题型:解答题
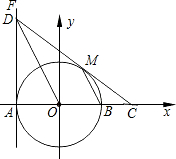 如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=$\frac{7}{6}$ | B. | x=-$\frac{7}{6}$ | C. | x=-$\frac{6}{7}$ | D. | x=$\frac{6}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-m-n)(-m+n) | B. | $(\frac{1}{2}x+1)(-\frac{1}{2}x-1)$ | C. | (3x-y)(-3x+y) | D. | (2a+b)(2b-a) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com