
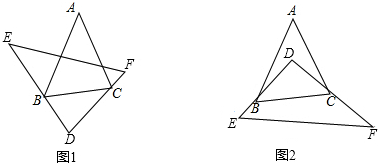
分析 (1)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠CBD+∠ACB+∠BCD,利用三角形内角和定理得出∠ABC+∠ACB=180°-∠A=180°-50°=130°;根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=100°,得出∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=130°+100°=230°;
(2)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠ACB-(∠BCD+∠CBD)的度数.根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=n°;根据三角形内角和定理得,∠ABC+∠ACB=180°-∠A=(180-m)°,得出∠ABD+∠ACD=∠ABC+∠ACB-(∠BCD+∠CBD)=(180-m-n)°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
解答 解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=50°
∴∠ABC+∠ACB=180°-50°=130°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°-∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°-∠D
∴∠CBD+∠BCD=∠E+∠F=100°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=130°+100°=230°.
(2)∠ABD+∠ACD=(180-m-n)°;
理由如下:
∵∠E+∠F=n°
∴∠CBD+∠BCD=∠E+∠F=n°
∴∠ABD+∠ACD=∠ABC+∠ACB-(∠BCD+∠CBD)=(180-m-n)°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
点评 此题考查三角形内角和定理,外角性质.熟练掌握这些性质是解题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
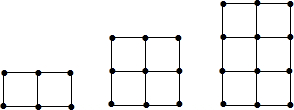
| 第几个图形 | 1 | 2 | 3 | 4 | … |
| 火柴棒根数 | 7 | 12 | 17 | 22 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com