
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.

【考点】全等三角形的判定与性质;旋转的性质.
【专题】几何综合题.
【分析】(1)由旋转的性质 可得:CD=CE,再根据同角的余角相等可证明∠BCD=∠FCE,再根据全等三角形的判定方法即可证明△BCD≌△FCE;
可得:CD=CE,再根据同角的余角相等可证明∠BCD=∠FCE,再根据全等三角形的判定方法即可证明△BCD≌△FCE;
(2)由(1)可知:△BCD≌△FCE,所以∠BDC=∠E,易求∠E=90°,进而可求出∠BDC的度数.
【解答】(1)证明:∵将线段CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=90°﹣∠ACD=∠FCE,
在△BCD和△FCE中,
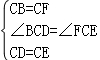 ,
,
∴△BCD≌△FCE(SAS).
(2)解:由(1)可知△BCD≌△FCE,
∴∠BDC=∠E,∠BCD=∠FCE,
∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,
∵EF∥CD,
∴∠E=180°﹣∠DCE=90°,
∴∠BDC=90°.
【点评】本题考查了全等三角形的判定和性质、同角的余角相等、旋转的性质、平行线的性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
某班分两组去两处植树,第一组22人,第二组26人,现在第一组植树遇到困难,需第二组支援,问从第二组调多少人去第一组才能使第一组人数是第二组的2倍,设抽调x人,则可列方程( )
A. 22+x=2×26; B. 22+x=2(26-x);
C. 2(22+x)=26-x; D. 22=2(26-x);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com