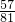
分析:观察可得,分数的分母是分数所在的序数加1的平方,后一个分数的分子与前一个分数的分子的差是连续的偶数,找出分子的变化规律的通项表示,然后求出第8个分数的分子,即可得解.
解答:∵4=(1+1)
2,9=(2+1)
2,16=(3+1)
2,25=(4+1)
2,36=(5+1)
2,
∴第8个分数的分母是(8+1)
2=81,
设第n个数的分子为a
n,则a
1=1,
a
2-a
1=3-1=2=2×1,
a
3-a
2=7-3=4=2×2,
a
4-a
3=13-7=6=2×3,
a
5-a
4=21-13=8=2×4,
…,
a
n-a
n-1=2(n-1),
所以,a
1+(a
2-a
1)+(a
3-a
2)+(a
4-a
3)+(a
5-a
4)+…+(a
n-a
n-1)=1+2+4+6+8+…+2(n-1),
即a
n=1+

=1+n(n-1)=n
2-n+1,
当n=8时,a
8=8
2-8+1=57,
所以,第8个数是
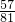
.
故答案为:
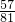
.
点评:本题是对数字变化规律的考查,仔细观察,分母的变化规律比较简单,关键是分子的变化规律,观察出后一个分数的分子与前一个分数的分子的差成偶数规律变化是解题的关键.

 ,
,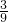 ,
, ,
, ,
,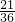 ,…,则第8个数是________.
,…,则第8个数是________.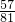
 =1+n(n-1)=n2-n+1,
=1+n(n-1)=n2-n+1,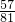 .
.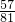 .
.
