
 x2+
x2+ x+n-5的图象与x轴交于点A、B,与y轴交于点C,其中点A在点B的左边,若∠ACB=90°,OC>OA且
x+n-5的图象与x轴交于点A、B,与y轴交于点C,其中点A在点B的左边,若∠ACB=90°,OC>OA且 +
+ =
= .
. =
=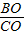 ,
, +
+ =
= ,
,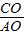 =
= ,
,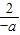 +
+ =
= ,
, •OC•AB=5,
•OC•AB=5, x2+
x2+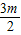 x+2,得m=1,
x+2,得m=1, x2+
x2+ x+2;
x+2; x2+
x2+ x+2=-
x+2=- (x-
(x- )2+
)2+ ,
, (x-k)2+
(x-k)2+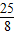 ,则这图象的形式、大小保持不变,
,则这图象的形式、大小保持不变,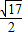 ,
, (x-
(x-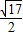 )2+
)2+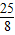 ①或y=-
①或y=- (x+
(x+ )2+
)2+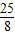 ②
② (x-
(x-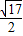 )2+
)2+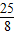 =0的两根,
=0的两根, -
- ,x2=
,x2=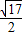 +
+ ,
, S△ABC,同理对于②也成立.
S△ABC,同理对于②也成立.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源:2009年江西省上饶市玉山县中考数学模拟试卷(解析版) 题型:填空题
 ,且过点(0,3),那么这个一次函数的解析式是 .
,且过点(0,3),那么这个一次函数的解析式是 .查看答案和解析>>
科目:初中数学 来源:2009年江西省上饶市玉山县中考数学模拟试卷(解析版) 题型:填空题
 x2-4x+3写成y=a(x-k)2+h的形式是 .
x2-4x+3写成y=a(x-k)2+h的形式是 .查看答案和解析>>
科目:初中数学 来源:2009年江西省上饶市玉山县中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com