
һ�һ�����ԭ��ÿ������Ϊ120��Ԫ���ӽ���1����װʹ�û��վ����豸(��װʱ�䲻��)��һ��������˻�������һ������ԭ�ϳɱ����ݲ��㣬ʹ�û��վ����豸���1��x��(1��x��12)���������ƽ��ֵw(��Ԫ)����w��10x��90���ڶ�����������ȶ��ڵ�1��ĵ�12���µ�ˮƽ��
(1)��ʹ�û��վ����豸���1��x��(1��x��12)�������Ϊy��д��y����x�ĺ�����ϵʽ������ǰ�����µ�����͵���700��Ԫ��
(2)��xΪ��ֵʱ��ʹ�û��վ����豸���1��x�µ�������벻��װ���վ����豸ʱx���µ��������ȣ�
(3)��ʹ�û��վ����豸������������ܺͣ�
��1��5���£���2��3����3��6360��Ԫ��
���������������1����Ϊʹ�û��վ����豸���1��x�£�1��x��12�����������ƽ��ֵw����Ԫ������w=10x��90������y=xw=x��10x��90����Ҫ��ǰ�����µ������=700��Ԫ������y=700�����÷��̼��ɽ�����⣻��2����Ϊԭ��ÿ������Ϊ120��Ԫ��ʹ�û��վ����豸���1��x�µ�������벻��װ���վ����豸ʱx���µ��������ȣ�������y=120x����֮��������𰸣���3����Ϊʹ�û��վ����豸���һ�����������=12����10��12+90����������ǵĺͼ��ɣ�
����������⣺(1)y��xw��x(10x��90)��10x2��90x��
10x2��90x��700��
��ã�x��5��14(�������⣬��ȥ)��
��ǰ5���µ�����͵���700��Ԫ��
(2)10x2��90x��120x��
��ã�x��3��0(�������⣬��ȥ)��
�𣺵�xΪ3ʱ��ʹ�û��վ����豸���1��x�µ�������벻��װ���վ����豸ʱx���µ��������ȣ�
(3)��һ��ȫ��������ǣ�12(10��12��90)��2520(��Ԫ)��
ǰ11���µ��������ǣ�11(10��11��90)��2200(��Ԫ)��
���12�µ�������2520��2200��320��Ԫ��
�ڶ���������ܺ���12��320��3840��Ԫ��
2520��3840��6360(��Ԫ)��
��ʹ�û��վ����豸������������ܺ���6360��Ԫ��
���㣺һԪ���η��̵�Ӧ��


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
����ˮλʱ�������߹����µ�ˮ���ΪBC=20m��ˮ������3m�ﵽ�õؾ���ˮλDEʱ������ˮ���Ϊ10m.����BC����ֱ��Ϊx�ᣬBC�Ĵ�ֱƽ����Ϊy�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ.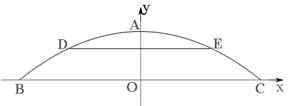
��1�����ſ������ߵĺ�����ϵʽ��
��2�����ˮλ��0.2m/h���ٶȳ������ǣ���ô�ﵽ����ˮλ���ٹ��ʱ����ſ�����û��
��3�����ﵽ����ˮλʱ��һ��װ�з�Ѵ���ĵĴ���¶��ˮ�沿�ֵĿ�Ϊ4m����Ϊ0.75m��ͨ������˵���ô��ܷ�˳��ͨ���˹��ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���� .
.
��1��m= ʱ������ͼ����x��ֻ��һ�����㣻
��2��mΪ��ֵʱ������ͼ����x��û�н��㣻
��3��������ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���ҡ�ABC�����Ϊ4����m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������ ��
�� ���ཻ��
���ཻ�� ��
�� ���㣨��
���㣨�� �ڵ�
�ڵ� ����ࣩ����
����ࣩ���� ���ཻ�ڵ�
���ཻ�ڵ� ��
��
��1���� ������Ϊ ����
������Ϊ ���� ������Ϊ ��
������Ϊ ��
��2���� ������������Ƿ���ڵ�
������������Ƿ���ڵ� ��ʹ�Ե�
��ʹ�Ե� ��
�� ��
�� �������������
Ϊ������������� ���ƣ������ڣ������
���ƣ������ڣ������ �����꣬�������ڣ���˵�����ɣ�
�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ƽ��ֱ������ϵ�У��Ե�C��2��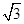 ��ΪԲ�ģ���2Ϊ�뾶��Բ��
��ΪԲ�ģ���2Ϊ�뾶��Բ�� �ύ��A��B���㣮
�ύ��A��B���㣮
��1����A��B��������ꣻ
��2�������κ��� ��ͼ����A��B����ȷ���˶��κ����Ľ���ʽ��
��ͼ����A��B����ȷ���˶��κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
���κ���y=x2+bx+c��ͼ���㣨4,3��,��3,0����
��1��b= ,c= ��
��2��ѡȡ�ʵ���������д�±�,������ͼ��ֱ������ϵ�л����ú�����ͼ��
| x | �� | | | | | | �� |
| y | �� | | | | | | �� |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ���y1=ax2��bx��3��ͼ����A��2��-3����B��-1��0������y�ύ�ڵ�C����x����һ���㽻�ڵ�D.
��1������κ����Ľ���ʽ��
��2�����C����D�����ꣻ
��3����һ��ֱ��y2,����C��D���㣬��ֱ��д��y1��y2ʱ�� ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�������� ��
�� �ύ�ڵ�A(��1��0)��B(3��0)����
�ύ�ڵ�A(��1��0)��B(3��0)���� �ύ�ڵ�C(0��3)��
�ύ�ڵ�C(0��3)��
(1)�������ߵĽ���ʽ������D�����ꣻ
(2)��PΪ�߶�BD�ϵ�һ�����㣬��P�ĺ�����Ϊm�����ú�m�Ĵ���ʽ��ʾ��P�������ꣻ
(3)����P��PM��x���ڵ�M�����ı���PMAC����������ֵ�ʹ�ʱ��P�����ꣻ
(4)����F�ǵ�һ�����������ϵ�һ�����㣬����F��FQ��AC��x���ڵ�Q������F������Ϊ ʱ���ı���FQAC��ƽ���ı��Σ�����F������Ϊ ʱ���ı���FQAC�ǵ�������(ֱ��д���������д������)��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com