
 如图,从一个边长为1米的正方形铁皮中剪下一个扇形.
如图,从一个边长为1米的正方形铁皮中剪下一个扇形. 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
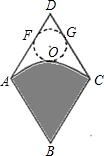 如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.
如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.查看答案和解析>>
科目:初中数学 来源: 题型:
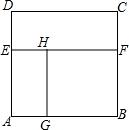 如图,从一个边长为a的正方形纸片ABCD中剪去一个宽为b的长方形CDEF,再从剩下的纸片中沿平行短边的方向剪去一个边长为c的正方形BFHG,若长方形CDEF与AGHE的面积比是3:2,那么
如图,从一个边长为a的正方形纸片ABCD中剪去一个宽为b的长方形CDEF,再从剩下的纸片中沿平行短边的方向剪去一个边长为c的正方形BFHG,若长方形CDEF与AGHE的面积比是3:2,那么| b | a |
查看答案和解析>>
科目:初中数学 来源: 题型:
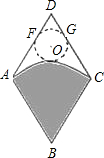 如图,从一个边长为2的菱形铁皮中剪下一个圆心角为60°的扇形.
如图,从一个边长为2的菱形铁皮中剪下一个圆心角为60°的扇形.查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省杭州市九年级12月月考数学试卷(解析版) 题型:解答题
(本题10分)如图,从一个边长为1米的正方形铁皮中剪下一个扇形.
(1)求这个扇形的面积(结果保留 );
);
(2)能否从剩下的余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com