

分析 (1)只要证明△ABG≌△CBE即可;
(2)首先证明△ABG≌△CBE,可得AG=CE,∠GAB=∠CEB,由∠ABC=90°,可得∠BCE+∠BMC=90°,由∠AMH=∠BMC,推出∠GAB+∠AMH=90°,可得∠AHM=90°;
(3)连接EG.首先证明∠H=90°,由勾股定理可得:EG2=BG2+BE2=2×(2$\sqrt{13}$)2=104,由EH=5GH,可得GH2+( 5GH)2=104,解得:GH=2;
解答 解:(1)证明:如图1中,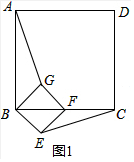
∵四边形ABCD和四边形BEFG都是正方形,
∴AB=BC,BG=BE,∠ABC=∠GBE=90°,
∴∠ABC-∠GBC=∠GBE-∠GBC,
∴∠ABG=∠CBE,
∴△ABG≌△CBE,
∴AG=CE.
(2)如图2中,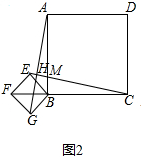
同(1)∴AB=BC,BG=BE,∠ABC=∠GBE=90°,
∴∠ABC+∠ABE=∠GBE+∠ABE,
∴∠ABG=∠CBE,
∴△ABG≌△CBE,
∴AG=CE,∠GAB=∠CEB,
∵∠ABC=90°,
∴∠BCE+∠BMC=90°,
∵∠AMH=∠BMC,
∴∠GAB+∠AMH=90°,
∴AHM=90°,
∴AG⊥EC.
(3)连接EG.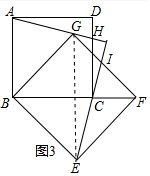
同(1)可得△ABG≌△CBE,
∴∠AGB=∠CEB,
∵∠BGF=∠BEF=90°,
∴∠AGB+∠HGI=∠BEC+∠IEF=90°,
又∵∠GIH=∠EIF,
∴∠HGI=∠FEI,
∴∠H=∠EFI,
∵∠EFG=90°,
∴∠H=90°,
∴GH2+EH2=GE2,
∵在正方形BEFG中BG=BE,∠GBE=90°,BG=2$\sqrt{13}$.
由勾股定理可得:EG2=BG2+BE2=2×(2$\sqrt{13}$)2=104,
∵EH=5GH,
∴GH2+( 5GH)2=104,
解得:GH=2,
∴EH=10.
点评 本题考查四边形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组别 | 成绩(米) | 频数 |
| A | 5.25≤x<6.25 | 5 |
| B | 6.25≤x<7.25 | 10 |
| C | 7.25≤x<8.25 | a |
| D | 8.25≤x<9.25 | 15 |
| E | 9.25≤x<10.25 | b |

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
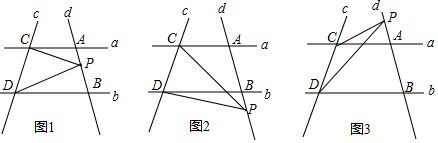
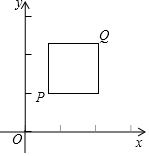 在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.
在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
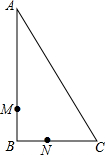 如图,在直角三角形ABC中,∠B=90°,点M、N分别在边BA,BC上,且BM=BN.
如图,在直角三角形ABC中,∠B=90°,点M、N分别在边BA,BC上,且BM=BN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com