
���� ��1����y=0��ֱ�ӽⷽ�̼��ɣ�
��2�����ݡ�CBO���DAE�����ҡ�COB=��DEA=90�㣬�õ�$\frac{CO}{DE}$=$\frac{OB}{AE}$��$\frac{CO}{AE}$=$\frac{OB}{DE}$���Ӷ��õ�m��a�Ĺ�ϵ��
��3������������ͼ��ֻ�п��ڷ���ͬ���Գ�����ͬ�ɵó����ۣ�
��� 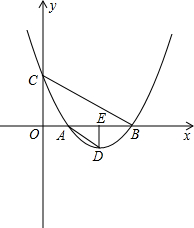 �⣺��1����ͼ����y=0ʱ��a��x-m��2-a��x-m��=0����ã�x1=m��x2=m+1��
�⣺��1����ͼ����y=0ʱ��a��x-m��2-a��x-m��=0����ã�x1=m��x2=m+1��
�ߵ�A�ڵ�B����࣬
��A��m��0����B��m+1��0����
��2����x=0ʱ��y=am2+am��
�ɵã�C��0��am2+am����
y=a��x-m��2-a��x-m��=a��x-$\frac{2m+1}{2}$��2-$\frac{a}{4}$��
���D��������$\frac{2m+1}{2}$��-$\frac{a}{4}$����
�ߡ�CBO���DAE�����ҡ�COB=��DEA=90�㣬
��$\frac{CO}{DE}$=$\frac{OB}{AE}$��$\frac{CO}{AE}$=$\frac{OB}{DE}$��
��|$\frac{{am}^{2}+am}{-\frac{a}{4}}$|=|$\frac{m+1}{\frac{2m+1}{2}-m}$|��|$\frac{{am}^{2}+am}{\frac{2m+1}{2}-m}$|=|$\frac{m+1}{-\frac{a}{4}}$|��
���a2m=��2����a��0��m��-1�����ߣ���m=��$\frac{1}{2}$ʱ��a��ȡһ�з���ʵ����
��3��x������ֱ�ߣ�x=$\frac{2m+1}{2}$��
�ʴ�Ϊx=$\frac{2m+1}{2}$��
���� ���⿼���˶��κ����ۺ��⣬�漰�����뷽�̵Ĺ�ϵ�����������ε��ж������ʵȣ��ѶȽϴ�


 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
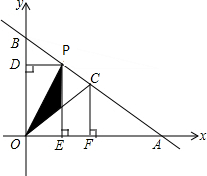 ��ͼ����A��B����ֱ�Ϊ��8��0������0��6������C���߶�AB���е㣬��P������BA��һ���㣬��P��PD��y����D��PE��x����E����OE=t������OEPD���POC�غϲ��ֵ����ΪS��
��ͼ����A��B����ֱ�Ϊ��8��0������0��6������C���߶�AB���е㣬��P������BA��һ���㣬��P��PD��y����D��PE��x����E����OE=t������OEPD���POC�غϲ��ֵ����ΪS���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����ABC�У�DE��BC��AE��EB=2��3������AED�������4m2�����ı���DEBC�����Ϊ��������
��ͼ��ʾ����ABC�У�DE��BC��AE��EB=2��3������AED�������4m2�����ı���DEBC�����Ϊ��������| A�� | 6m2 | B�� | 21m2 | C�� | 3m2 | D�� | 5m2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
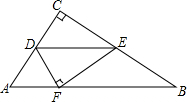 ��ͼ����ABC�У���C=90�㣬AC=6��BC=8��D��E�ֱ���AC��BC����DE��AB������ABC��DE�۵���ʹC������б��AB�ϵ�F������AF�ij��ǣ�������
��ͼ����ABC�У���C=90�㣬AC=6��BC=8��D��E�ֱ���AC��BC����DE��AB������ABC��DE�۵���ʹC������б��AB�ϵ�F������AF�ij��ǣ�������| A�� | 3.6 | B�� | 4 | C�� | 4.8 | D�� | 6.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
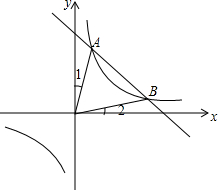 ��ͼ������y1=$\frac{{k}_{1}}{x}$��ͼ���뺯��y2=k2x+b��ͼ����A��B���㣬��֪A�������Ϊ��1��4����
��ͼ������y1=$\frac{{k}_{1}}{x}$��ͼ���뺯��y2=k2x+b��ͼ����A��B���㣬��֪A�������Ϊ��1��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
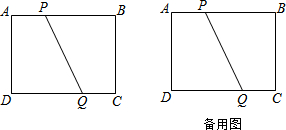
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 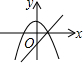 | B�� | 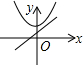 | C�� | 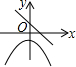 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O�İ뾶Ϊ5��ABΪ��O���ң�OC��AB�ڵ�C����OC=3����AB�ij�Ϊ8��
��ͼ����O�İ뾶Ϊ5��ABΪ��O���ң�OC��AB�ڵ�C����OC=3����AB�ij�Ϊ8���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com