【题目】如图，梯形的上底为a2+2a﹣10，下底为3a2﹣5a﹣80，高为40．（π取3）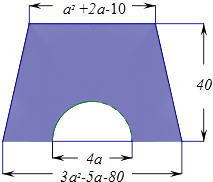 
（1）用式子表示图中阴影部分的面积；
（2）当a=10时，求阴影部分面积的值．
【答案】
（1）解：∵梯形的上底为a2+2a﹣10，下底为3a2﹣5a﹣80，高为40，半圆的直径为4a，
∴阴影部分的面积= 
（a2+2a﹣10+3a2﹣5a﹣80）×40﹣ π（ 
）2，
=80a2﹣60a﹣1800﹣2a2π，
=80a2﹣60a﹣1800﹣2a2×3，
=74a2﹣60a﹣1800
（2）解：当a=10时，74a2﹣60a﹣1800=74×102﹣60×10﹣1800=5000
【解析】（1）根据梯形的面积= （上底+下底）×高，阴影部分的面积等于梯形的面积减去半圆的面积，列式进行计算即可得解；（2）把a=10代入（1）中的代数式进行计算即可得解．
【考点精析】本题主要考查了代数式求值的相关知识点，需要掌握求代数式的值，一般是先将代数式化简，然后再将字母的取值代入；求代数式的值，有时求不出其字母的值，需要利用技巧，“整体”代入才能正确解答此题．
科目：初中数学 来源： 题型：
【题目】某工厂第一车间有x人，第二车间比第一车间人数的 
少30人，如果从第二车间调出10人到第一车间，那么：
（1）两个车间共有多少人？
（2）调动后，第一车间的人数比第二车间多多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料，回答问题：
材料
题1：经过某十字路口的汽车，可能直行，也可能向左转或向右转．如果这三种可能性的大小相同，求三辆汽车经过这个十字路口时，至少要两辆车向左转的概率
题2：有两把不同的锁和三把钥匙，其中两把钥匙分别能打开这两把锁（一把钥匙只能开一把锁），第三把钥匙不能打开这两把锁．随机取出一把钥匙开任意一把锁，一次打开锁的概率是多少？
我们可以用“袋中摸球”的试验来模拟题1：在口袋中放三个不同颜色的小球，红球表示直行，绿球表示向左转，黑球表示向右转，三辆汽车经过路口，相当于从三个这样的口袋中各随机摸出一球.
问题：
（1）事件“至少有两辆车向左转”相当于“袋中摸球”的试验中的什么事件？
（2）设计一个“袋中摸球”的试验模拟题2，请简要说明你的方案
（3）请直接写出题2的结果．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了美化文山市民的生活环境，环保局将一段长为360米的河道整治任务交给甲、乙两个工程队接力完成，共用时20天，已知甲工程队每天整治24米，乙工程队每天整治16米，求甲、乙两个工程队分别整治了多少天？
查看答案和解析>>
科目：初中数学 来源： 题型：
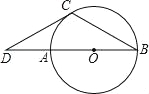
【题目】已知：如图，AB是⊙O的直径，BC是弦，∠B=30°，延长BA到D，使∠BDC=30°．
（1）求证：DC是⊙O的切线；
（2）若AB=2，求DC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两名男同学练习投掷实心球，每人投了10次，平均成绩均为7.5米，方差分别为s甲2＝0.2，S乙2＝0.08，成绩比较稳定的是_____(填“甲”或“乙”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com