
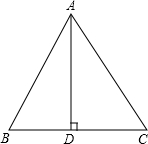
 已知,如图,等边三角形ABC,AD为BC边上的高线,若AB=2,求△ABC的面积.
已知,如图,等边三角形ABC,AD为BC边上的高线,若AB=2,求△ABC的面积. 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
 类似地你可以得到:“满足
类似地你可以得到:“满足查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(江苏南京) 题型:解答题
学习《图形的相似》后,我们可以探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件.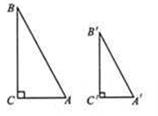
(1)“对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,两个直角三角形全等”,类似地,你可以得到“满足_____,或_____,两个直角三角形相似”;
(2)“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,你可以得到满足_____两个直角三角形相似”.请结合下列所给图形,写出已知,并完成说理过程.
已知:如图,_____.试说明Rt△ABC∽Rt△A/B/C/.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市考数学一模试卷 题型:选择题
已知:如图,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若 ,则等边三角
,则等边三角
形ABC的边长为

A. 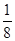 B.
B.  C.
C.
 D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若![]() ,则等边三角
,则等边三角
形ABC的边长为
A. ![]() B.
B. ![]() C.
C.![]() D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com