Question

学校举办“迎奥运”知识竞赛，设一、二、三等奖共12名，奖品发放方案如下表：

一等奖	二等奖	三等奖
1盒福娃和1枚徽章	1盒福娃	1枚徽章

用于购买奖品的总费用不少于1000元但不超过1100元，小明在购买“福娃”和微章前，了解到如下信息：

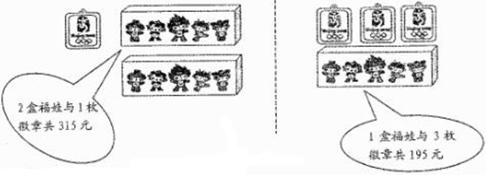
（1）求一盒“福娃”和一枚徽章各多少元？

（2）若本次活动设一等奖2名，则二等奖和三等奖应各设多少名？

 

Answer 1

【答案】

（1）一盒“福娃”150元，一枚徽章15元；（2）二等奖4名，三等奖6名

【解析】

试题分析：（1）设一盒“福娃”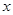元，一枚徽章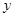元，根据2盒福娃与1枚微章共315元，1盒福娃与3枚微章共195元，即可列方程组求解；

（2）设二等奖m名，则三等奖（10—m）名，根据用于购买奖品的总费用不少于1000元但不超过1100元，即可列不等式组求解.

（1）设一盒“福娃”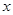元，一枚徽章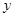元，由题意得

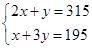，解得 

答：一盒“福娃”150元，一枚徽章15元；

（2）设二等奖m名，则三等奖（10—m）名，

 

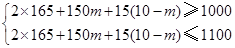
解得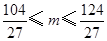

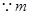是整数，

∴m＝4，

∴10－m＝6．

答：二等奖4名，三等奖6名．

考点：本题考查的是二元一次方程组的应用，一元一次不等式组的应用

点评：解答本题的关键是读懂题意，找准不等关系列出不等式组，并注意未知数的取值是正整数．