
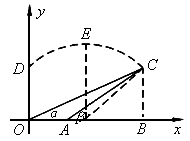
如图所示,这是某防空部队进行射击训练时在直角坐标系中的示意图,在地面O、A两个观测点测得空中固定目标C的仰角分别为α和β,OA=1千米,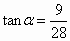 ,
, .位于O点正上方
.位于O点正上方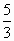 千米D处的直升机向目标C发射导弹,该导弹运行达到地面最大高度3千米时,相应的水平距离为4千米(即图中的E点).
千米D处的直升机向目标C发射导弹,该导弹运行达到地面最大高度3千米时,相应的水平距离为4千米(即图中的E点).
(1)若导弹运动轨道为一抛物线,求抛物线的函数关系式;
(2)说明按(1)中轨道运行的导弹能否击中目标C的理由.
|
解法 1:(1)设导弹动力轨道的抛物线的函数关系式是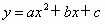 . .
由题意知,抛物线的顶点坐标为 E(4,3),对称轴是直线x=4.因为点 D(0,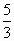 )在这条抛物线上,所以点D关于直线x=4的对称轴点 )在这条抛物线上,所以点D关于直线x=4的对称轴点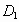 也在这条抛物线上,其坐标为(8, 也在这条抛物线上,其坐标为(8,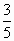 ). ).
将点 E、D、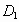 三点的坐标代入 三点的坐标代入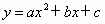 ,得 ,得
解这个方程组,得 所以导弹运行轨道的抛物线的函数关系式是 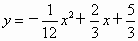 . .
(2) 设C点的坐标为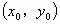 ,过点C作CB⊥x轴,垂足为点B. ,过点C作CB⊥x轴,垂足为点B.
因为 OA=1,所以tanα=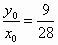 , ,
tan β=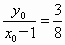 . .
即 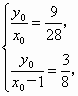
解得 所以点 C的坐标为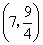 . .
因为,当 x=7时,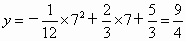 . .
所以点 C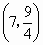 在抛物线 在抛物线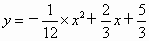 上,所以导弹能击中目标C. 上,所以导弹能击中目标C.
解法 2:(1)由题意知,抛物线的顶点坐标E(4,3).所以可设导弹运行轨道的抛物线的函数关系式为 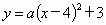 . .
因为点 D(0,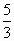 )在抛物线上,所以 )在抛物线上,所以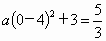 . 解得 . 解得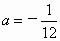 . .
所以导弹运行的抛物线的函数关系式为 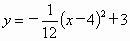 ,即 ,即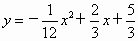 . .
(2) 设C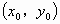 ,过点C作CB⊥x轴,垂足为点B,则OB= ,过点C作CB⊥x轴,垂足为点B,则OB=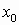 ,BC= ,BC=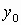 . .
因为 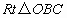 ,tanα= ,tanα=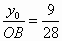 ,所以OB= ,所以OB=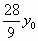 . .
因为在  中, 中,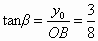 ,所以 ,所以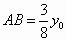 . .
因为 OA=1,即OB-AB=1,所以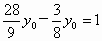 ,解得 ,解得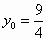 . .
所以 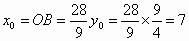 .所以点C的坐标为 .所以点C的坐标为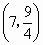 . .
把 x=7代入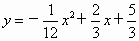 ,得 ,得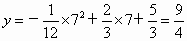 . .
所以点 C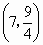 在抛物线上,所以导弹能击中目标C. 在抛物线上,所以导弹能击中目标C. |
|
解决本题的关键是求抛物线的函数关系式,解题时注意到点 E是抛物线的顶点,巧设顶点式,从而既简单又迅速的得出问题的答案.(2)题则巧用转化思想,将能否击中目标C转化为判断点C是否在抛物线上. |


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源:同步单元练习数学 九年级下册 题型:044
如图所示,这是某防空部队进行射击训练时在平面直角坐标系中的示意图,固定目标B的坐标是![]() ,位于地面O点正上方A处的直升飞机向目标B发射导弹,导弹的高度h(km)可用公式h=
,位于地面O点正上方A处的直升飞机向目标B发射导弹,导弹的高度h(km)可用公式h=![]() x2+
x2+![]() x+
x+![]() (x是导弹离开O点的水平距离)表示.
(x是导弹离开O点的水平距离)表示.

(1)导弹能否击中目标B,为什么?
(2)点A离地面有多高?
(3)说明方程![]() x2+
x2+![]() x+
x+![]() =0的根的实际意义.
=0的根的实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com