
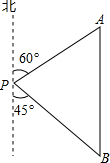
 五一期间,小红到美丽的世界地质公园湖光岩参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果保留根号)
五一期间,小红到美丽的世界地质公园湖光岩参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果保留根号) 分析 由已知作PC⊥AB于C,可得△ABP中∠A=60°∠B=45°且PA=100m,要求AB的长,可以先求出AC和BC的长.
解答 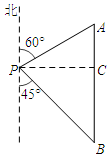 解:过点P作PC⊥AB于C,则∠ACP=∠BCP=90°,∠APC=30°,∠BPC=45°.
解:过点P作PC⊥AB于C,则∠ACP=∠BCP=90°,∠APC=30°,∠BPC=45°.
在Rt△ACP中,∵∠ACP=90°,∠APC=30°,AP=100,
∴AC=$\frac{1}{2}$AP=50,PC=$\sqrt{3}$AC=50$\sqrt{3}$.
在Rt△BPC中,∵∠BCP=90°,∠BPC=45°,
∴BC=PC=50$\sqrt{3}$.
∴AB=AC+BC=(50+50$\sqrt{3}$)(米).
答:景点A与B之间的距离为(50+50$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用,对于解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


科目:初中数学 来源: 题型:填空题
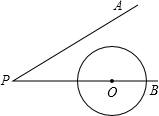 如图,∠APB=30°,圆心在边PB上的⊙O半径为2cm,OP=6cm,若⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的最少距离为2cm.
如图,∠APB=30°,圆心在边PB上的⊙O半径为2cm,OP=6cm,若⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的最少距离为2cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
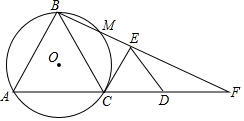 如图,C为线段AD上一点,△ABC和△CDE都是等边三角形,连接BE并延长,交AD长线于F,△ABC的外接圆⊙O交BF于点M.
如图,C为线段AD上一点,△ABC和△CDE都是等边三角形,连接BE并延长,交AD长线于F,△ABC的外接圆⊙O交BF于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护的问题的电话最多,共70个,请回答下列问题.
如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护的问题的电话最多,共70个,请回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
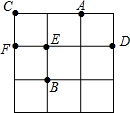 如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是( )
如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是( )| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com