
 的长为4,宽为3,以长
的长为4,宽为3,以长 所在的直线为x轴,O为坐标原点建立平面直角坐标系;点P是OA边上的动点(与点
所在的直线为x轴,O为坐标原点建立平面直角坐标系;点P是OA边上的动点(与点 不重合),现将
不重合),现将 沿PC翻折得到
沿PC翻折得到 ,再在边
,再在边 上选取适当的点D,将
上选取适当的点D,将 沿
沿 翻折,得到
翻折,得到 ,使得直线
,使得直线 重合.
重合. 上,如图①,求点
上,如图①,求点 的坐标,并求过此三点的抛物线的函数关系式;
的坐标,并求过此三点的抛物线的函数关系式; 的内部,如图②,设
的内部,如图②,设 当x为何值时,y取得最大值?
当x为何值时,y取得最大值? 三点的抛物线上是否存在点Q,使
三点的抛物线上是否存在点Q,使 是以
是以 为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标。
为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标。
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
 知矩形纸片ABCD(矩形纸片要足够长),我们按如下步骤操作可以得到一个特定的角:
知矩形纸片ABCD(矩形纸片要足够长),我们按如下步骤操作可以得到一个特定的角:| A、60° | B、67.5° | C、72° | D、75° |
查看答案和解析>>
科目:初中数学 来源: 题型:
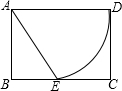 如图,已知矩形纸片ABCD,AD=2,AB=
如图,已知矩形纸片ABCD,AD=2,AB=| 3 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
已知矩形纸片![]() 的长为4,宽为3,以长
的长为4,宽为3,以长![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 为坐标原点建
为坐标原点建
立平面直角坐标系;点![]() 是
是![]() 边上的动点(与点
边上的动点(与点![]() 不重合),现将
不重合),现将![]() 沿
沿![]() 翻折
翻折
得到![]() ,再在
,再在![]() 边上选取适当的点
边上选取适当的点![]() 将
将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,使得
,使得
直线![]() 重合.
重合.
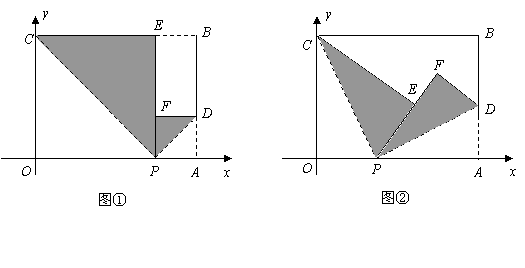
(1)若点![]() 落在
落在![]() 边上,如图①,求点
边上,如图①,求点![]() 的坐标,并求过此三点的抛物线的函数关系式;
的坐标,并求过此三点的抛物线的函数关系式;
(2)若点![]() 落在矩形纸片
落在矩形纸片![]() 的内部,如图②,设
的内部,如图②,设![]() 当
当![]() 为何值时,
为何值时,![]() 取得最大值?
取得最大值?
(3)在(1)的情况下,过点![]() 三点的抛物线上是否存在点
三点的抛物线上是否存在点![]() 使
使![]() 是以
是以![]() 为直角边的直角三角形?若不存在,说明理由;若存在,求出点
为直角边的直角三角形?若不存在,说明理由;若存在,求出点![]() 的坐标
的坐标
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知矩形纸片![]() 的长为4,宽为3,以长
的长为4,宽为3,以长![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 为坐标原点建
为坐标原点建
立平面直角坐标系;点![]() 是
是![]() 边上的动点(与点
边上的动点(与点![]() 不重合),现将
不重合),现将![]() 沿
沿![]() 翻折
翻折
得到![]() ,再在
,再在![]() 边上选取适当的点
边上选取适当的点![]() 将
将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,使得
,使得
直线![]() 重合.
重合.
(1)若点![]() 落在
落在![]() 边上,如图①,求点
边上,如图①,求点![]() 的坐标,并求过此三点的抛物线的函数关系式;
的坐标,并求过此三点的抛物线的函数关系式;
(2)若点![]() 落在矩形纸片
落在矩形纸片![]() 的内部,如图②,设
的内部,如图②,设![]() 当
当![]() 为何值时,
为何值时,![]() 取得最大值?
取得最大值?
(3)在(1)的情况下,过点![]() 三点的抛物线上是否存在点
三点的抛物线上是否存在点![]() 使
使![]() 是以
是以![]() 为直角边的直角三角形?若不存在,说明理由;若存在,求出点
为直角边的直角三角形?若不存在,说明理由;若存在,求出点![]() 的坐标
的坐标
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com