
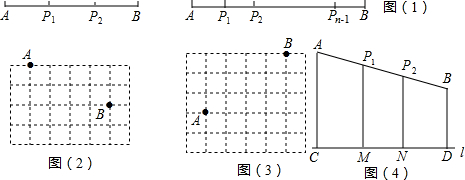
���� ��1�����������ε���λ�߶����Լ����ε���λ�߶������м��㣮
��2����P1M=x���ɣ�1���н��ۿɵ�$\frac{AC+{P}_{2}N}{2}$=x����P2N=2x-d1���ɣ�1���н��ۿɵ�$\frac{{P}_{1}M+BD}{2}$=P2N����$\frac{x+{d}_{2}}{2}$=2x-d1������1��P2��ֱ��l�ľ���ֱ�Ϊ$\frac{2{d}_{1}+{d}_{2}}{3}$��$\frac{{d}_{1}+2{d}_{2}}{3}$��
��3�����ݣ�1������2���Ĺ����ܽ��i��n�ȷֵ�Pi��ֱ��l�ľ��룮
��� �⣺��1������ͼ��2����AB��ֱ��l��ͬ�࣬���߶�AB���е�P��ֱ��l�ľ�����$\frac{1}{2}$����4+2��=3��cm����
�ʴ��ǣ�3��
����ͼ��3��������A��B��ֱ��l�ľ���ֱ���2����λ��5����λ����ô�߶�AB���е�P��ֱ��l�ľ����ǣ�$\frac{2+5}{2}$=$\frac{7}{2}$����λ����
�ʴ��ǣ�$\frac{7}{2}$��
���ɢ٢ڿ��Է��ֽ��ۣ�����A��B��ֱ��l�ľ���ֱ���h����λ��t����λ����ô�߶�AB���е�P��ֱ��l�ľ����� $\frac{h+t}{2}$��λ��
�ʴ��ǣ�$\frac{h+t}{2}$��
��2����ͼ��4������P1M=x���ɣ�1���н��ۿɵ�$\frac{AC+{P}_{2}N}{2}$=x��
��P2N=2x-d1��
�ɣ�1���н��ۿɵ�$\frac{{P}_{1}M+BD}{2}$=P2N����$\frac{x+{d}_{2}}{2}$=2x-d1��
�ⷽ�̵�x=$\frac{2{d}_{1}+{d}_{2}}{3}$��
��P2N=$\frac{{d}_{1}+2{d}_{2}}{3}$������1��P2��ֱ��l�ľ���ֱ�Ϊ$\frac{2{d}_{1}+{d}_{2}}{3}$��$\frac{{d}_{1}+2{d}_{2}}{3}$��
����A��B��ֱ��l�ľ���ֱ���d1��d2�����ã�1���еĽ������߶�AB�����ȷֵ�P1��P2��ֱ��l�ľ��� $\frac{2{d}_{1}+{d}_{2}}{3}$��$\frac{{d}_{1}+2{d}_{2}}{3}$��
��3������A��B��ֱ��l�ľ���ֱ���d1��d2����P1��P2����Pn-1Ϊ�߶�AB��n�ȷֵ㣬���i��n�ȷֵ�Pi��ֱ��l�ľ����� $\frac{��n-1��{d}_{1}+i{d}_{2}}{n}$��
���� ���⿼���������ľ���͵㵽ֱ�ߵľ��룮����ʱ��ע�����ν����ѧ˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| a | 0.000 001 | 0.001 | 1 | 1000 | 1000 000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
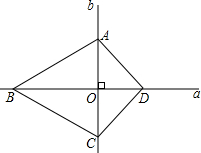 �Ķ�����Ӧ�ã������ڿα���ѧϰ����Ҫ��Ƚ�a��b�Ĵ�С��ϵ�����Խ���������������a-b��0��a��b��a-b��0��a��b��a-b=0��a=b��
�Ķ�����Ӧ�ã������ڿα���ѧϰ����Ҫ��Ƚ�a��b�Ĵ�С��ϵ�����Խ���������������a-b��0��a��b��a-b��0��a��b��a-b=0��a=b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢ڢ� | C�� | �ۢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com