解:(1)将点A(1,0)、点B(0,5)代入抛物线y=-x
2+bx+c可得:

,
解得:

,
故抛物线解析式为:y=-x
2-4x+5.
(2)由y=-x
2-4x+5,
令y=0,得-x
2-4x+5=0,
解得:x
1=-5,x
2=1,
则点C的坐标为(-5,0),
由抛物线顶点坐标可得点D的坐标为(-2,9),
过点D作DM⊥x轴于点M,
则S
△BCD=S
梯形BOMD+S
△DCM-S
△BOC=

×(5+9)×2+

×3×9-

×5×5=15;
(3)平移后点B的坐标为(a,5),点C的坐标为(-5+a,0),点D的坐标为(-2+a,9),
则直线BC的解析式为:y=x+5-a,
直线CD的解析式为:y=3x+15-3a,
直线BD的解析式为:y=-2x+2a+5,
①当点D在y轴左侧或y轴上时,0<a≤2,如图1所示:

点F的坐标为(0,2a+5),点E的坐标为(0,5-a),
过点B作BH⊥y轴于点H,
S
△BEF=

EF×BH=
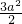
=

×15,
解得:a=

或-

(舍去);
②当点D在y轴右侧时,2<a<5,如图2所示:

点F的坐标为(0,-15-3a),点E的坐标为(0,5-a),
S
△CEF=

EF×OC=a
2-10a+25=

×15,
解得:a=5+

(舍去)或a=5-

,
综上可得:当a=

时,抛物线解析式为:y=-(x+2-

)
2+9;
当a=5-

时,抛物线解析式为:y=-(x-3+

)
2+9.
分析:(1)将点A、点B的坐标代入抛物线解析式可得出b、c的值,继而得出抛物线解析式;
(2)根据抛物线解析式求出点C、点A的坐标,过点D作DM⊥x轴于点M,根据S
△BCD=S
梯形BOMD+S
△DCM-S
△BOC,可得出△BCD的面积;
(3)分两种情况讨论,①点D在y轴左侧,②点D在y轴右侧,根据△BCD被y轴截得的三角形面积等于△BCD面积的

,可得出a的方程,解出即可得出答案.
点评:本题考查了二次函数的综合,涉及了待定系数法求二次函数解析式、三角形的面积及二次函数的几何变换,综合考察的知识点较多,同学们注意培养自己解答综合题的能力,能将所学知识融会贯通.

 已知:抛物线y=-x2+bx+c经过点A(1,0)、B(0,5).
已知:抛物线y=-x2+bx+c经过点A(1,0)、B(0,5). ,求此时抛物线的解析式.
,求此时抛物线的解析式. ,
, ,
, ×(5+9)×2+
×(5+9)×2+ ×3×9-
×3×9- ×5×5=15;
×5×5=15;
 EF×BH=
EF×BH=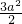 =
= ×15,
×15, 或-
或- (舍去);
(舍去);
 EF×OC=a2-10a+25=
EF×OC=a2-10a+25= ×15,
×15, (舍去)或a=5-
(舍去)或a=5- ,
, 时,抛物线解析式为:y=-(x+2-
时,抛物线解析式为:y=-(x+2- )2+9;
)2+9; 时,抛物线解析式为:y=-(x-3+
时,抛物线解析式为:y=-(x-3+ )2+9.
)2+9. ,可得出a的方程,解出即可得出答案.
,可得出a的方程,解出即可得出答案.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案