
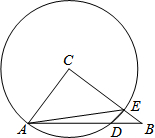
 如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
如图,已知在△ABC中,AC=15,AB=25,sin∠CAB= ,以CA为半径的⊙C与AB、BC分别交于点D、E,联结AE,DE.
,以CA为半径的⊙C与AB、BC分别交于点D、E,联结AE,DE.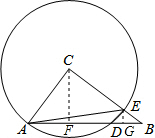 解:(1)过点作CF⊥AB于点F,
解:(1)过点作CF⊥AB于点F, ,
, =12,
=12, =
=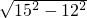 =9,
=9, =
=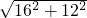 =20;
=20;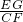 =
= ,
, =
=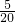 ,解得EG=3,
,解得EG=3, AD•EG=
AD•EG= ×18×3=27.
×18×3=27. 求出CF的长,由勾股定理求出AF的长,故可得出BF的长,在Rt△BCF中,根据勾股定理可求出BC的长;
求出CF的长,由勾股定理求出AF的长,故可得出BF的长,在Rt△BCF中,根据勾股定理可求出BC的长; AD•EG即可得出结论.
AD•EG即可得出结论.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com