
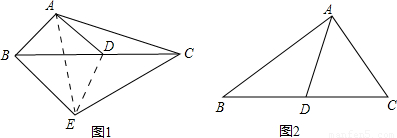
 证明:∵△ADC沿直线AD翻折后点C落在点E处,
证明:∵△ADC沿直线AD翻折后点C落在点E处,

科目:初中数学 来源: 题型:
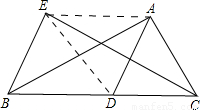
 (2011•郑州模拟)如图,家住A广场的王强同学每天经立交桥BC到学校,路线为A→B→C→D.为了缓解市区内一些主要路段交通拥挤的现状,要对立交桥BC封桥维修,他只能改道经立交桥FE到学校,路线为A→F→E→D.已知BC∥CE,AB⊥BF,CD⊥DE,AB=300米,BC=160米,∠AFB=37°,∠DCF=53°,请你计算王强同学上学的路程因改道增加了多少米?(结果保留整数)(温馨提示:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
(2011•郑州模拟)如图,家住A广场的王强同学每天经立交桥BC到学校,路线为A→B→C→D.为了缓解市区内一些主要路段交通拥挤的现状,要对立交桥BC封桥维修,他只能改道经立交桥FE到学校,路线为A→F→E→D.已知BC∥CE,AB⊥BF,CD⊥DE,AB=300米,BC=160米,∠AFB=37°,∠DCF=53°,请你计算王强同学上学的路程因改道增加了多少米?(结果保留整数)(温馨提示:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2006年福建省福州市一中招生综合素质测试数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com