
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 分别是线段AC、BC上的点,且四边形
分别是线段AC、BC上的点,且四边形![]() 为矩形.
为矩形.
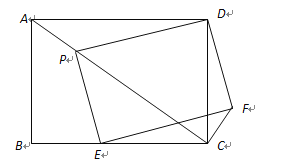
(Ⅰ)若![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长;
的长;
(Ⅱ)若![]() ,求
,求![]() 的长.
的长.
【答案】(Ⅰ)AP的长为4或5或![]() ;(Ⅱ)CF=
;(Ⅱ)CF=![]()
【解析】
试题分析:(Ⅰ)分情况CP=CD、PD=PC、DP=DC讨论即可得;
(Ⅱ)连结PF、DE,记PF与DE的交点为O,连结OC,通过证明△ADP∽△CDF,从而得![]() ,由AP=
,由AP=![]() ,从而可得CF=
,从而可得CF=![]() .
.
试题解析:(Ⅰ)在矩形ABCD中,AB=6,AD=8,∠ADC=90°,∴DC=AB=6, AC=![]() =10;
=10;
要使△PCD是等腰三角形,有如下三种情况:
(1)当CP=CD时,CP=6,∴AP=AC-CP=4 ;
(2)当PD=PC时,∠PDC=∠PCD,∵∠PCD+∠PAD=∠PDC+∠PDA=90°,∴∠PAD=∠PDA,∴PD=PA,∴PA=PC,∴AP=![]() ,即AP=5;
,即AP=5;
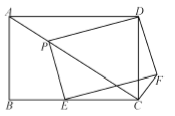
(3)当DP=DC时,过D作DQ⊥AC于Q,则PQ=CQ,∵S△ADC=![]() AD·DC=
AD·DC=![]() AC·DQ,∴DQ=
AC·DQ,∴DQ=![]() ,∴CQ=
,∴CQ=![]() ,∴PC=2CQ =
,∴PC=2CQ =![]() ,∴AP=AC-PC=
,∴AP=AC-PC=![]() .
.
综上所述,若△PCD是等腰三角形,AP的长为4或5或![]() ;
;
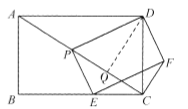
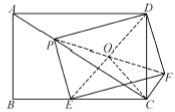
(Ⅱ)连结PF、DE,记PF与DE的交点为O,连结OC,
∵四边形ABCD和PEFD都是矩形,∴∠ADC=∠PDF=90°,即∠ADP+∠PDC=∠PDC+∠CDF,∴∠ADP=∠CDF,∵∠BCD=90°,OE=OD,∴OC=![]() ED,在矩形PEFD中,PF=DE,∴OC=
ED,在矩形PEFD中,PF=DE,∴OC=![]() PF,∵OP=OF=
PF,∵OP=OF=![]() PF,∴OC=OP=OF,∴∠OCF=∠OFC,∠OCP=∠OPC,又∵∠OPC+∠OFC+∠PCF=180°,∴2∠OCP+2∠OCF=180°,∴∠PCF=90°,即∠PCD+∠FCD=90°,在Rt△ADC中,∠PCD+∠PAD=90°,∴∠PAD=∠FCD,∴△ADP∽△CDF,∴
PF,∴OC=OP=OF,∴∠OCF=∠OFC,∠OCP=∠OPC,又∵∠OPC+∠OFC+∠PCF=180°,∴2∠OCP+2∠OCF=180°,∴∠PCF=90°,即∠PCD+∠FCD=90°,在Rt△ADC中,∠PCD+∠PAD=90°,∴∠PAD=∠FCD,∴△ADP∽△CDF,∴![]() ,∵AP=
,∵AP=![]() ,∴CF=
,∴CF=![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:

根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在可以不同年的条件下,下列结论叙述正确的是( )
A.400个人中至少有两人生日相同
B.300个人至少有两人生日相同
C.300个人一定没有两人生日相同
D.300个人一定有两人生日相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某次作业中得到如下结果:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
据此,小明猜想:对于任意锐角![]() ,均有
,均有![]() .
.
(Ⅰ)当![]() 时,验证
时,验证![]() 是否成立;
是否成立;
(Ⅱ)小明的猜想是否成立?若成立,若成立,请给予证明;若不成立,请举出一个反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
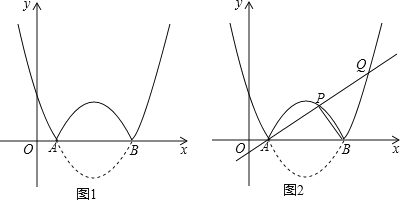
【题目】如图,抛物线l:y=![]() (x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.
(x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.
(1)若点A的坐标为(1,0).
①求抛物线l的表达式,并直接写出当x为何值时,函数的值y随x的增大而增大;
②如图2,若过A点的直线交函数的图象于另外两点P,Q,且S△ABQ=2S△ABP,求点P的坐标;
(2)当2<x<3时,若函数f的值随x的增大而增大,直接写出h的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com